题目内容
直线l过点(-1,0),圆C的圆心为C(2,0).
(Ⅰ)若圆C的半径为2,直线l截圆C所得的弦长也为2,求直线l的方程;
(Ⅱ)若直线l的斜率为1,且直线l与圆C相切;若圆C的方程.
(Ⅰ)若圆C的半径为2,直线l截圆C所得的弦长也为2,求直线l的方程;
(Ⅱ)若直线l的斜率为1,且直线l与圆C相切;若圆C的方程.
考点:圆的切线方程,直线与圆相交的性质
专题:综合题,直线与圆
分析:(Ⅰ)设直线l的方程为y=k(x+1),根据圆C的半径为2,直线l截圆C所得的弦长为2,利用点到直线的距离公式,建立方程,即可求直线l的方程;
(Ⅱ)根据直线l与圆C相切,利用点到直线的距离公式,可得圆C的半径r,从而可得圆C的方程.
(Ⅱ)根据直线l与圆C相切,利用点到直线的距离公式,可得圆C的半径r,从而可得圆C的方程.
解答:
解:(Ⅰ)设直线l的方程为y=k(x+1),则
∵圆C的半径为2,直线l截圆C所得的弦长为2,
∴圆心到直线l的距离为
,即
=
,解得k=±
,
即直线l的方程为y═±
(x+1);
(Ⅱ)∵直线l的斜率为1,
∴直线l的方程为y=x+1,
∵直线l与圆C相切,
∴r=
=
,
∴圆C的方程为(x-2)2+y2=
.
∵圆C的半径为2,直线l截圆C所得的弦长为2,
∴圆心到直线l的距离为
| 3 |
| |3k| | ||
|
| 3 |
| ||
| 2 |
即直线l的方程为y═±
| ||
| 2 |
(Ⅱ)∵直线l的斜率为1,
∴直线l的方程为y=x+1,
∵直线l与圆C相切,
∴r=
| 3 | ||
|
3
| ||
| 2 |
∴圆C的方程为(x-2)2+y2=
| 9 |
| 2 |
点评:本题考查直线与圆的位置关系,考查点到直线的距离公式,考查圆的性质,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
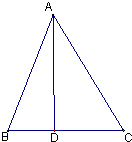 在△ABC中,角A、B、C所对应的边分别为a,b,c,AD是BC边上的高,且AD=BC
在△ABC中,角A、B、C所对应的边分别为a,b,c,AD是BC边上的高,且AD=BC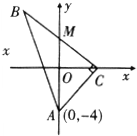 如图△ABC为直角三形,
如图△ABC为直角三形,