题目内容
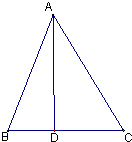 在△ABC中,角A、B、C所对应的边分别为a,b,c,AD是BC边上的高,且AD=BC
在△ABC中,角A、B、C所对应的边分别为a,b,c,AD是BC边上的高,且AD=BC(Ⅰ)若B=C,求sinA的值;
(Ⅱ)求
| c |
| b |
| b |
| c |
考点:正弦定理的应用
专题:解三角形
分析:(Ⅰ)根据B=C,即可求出tanA,然后求sinA的值;
(Ⅱ)根据正弦定理和辅助角公式将
+
进行化简,然后根据三角函数的图象和性质即可得到结论
(Ⅱ)根据正弦定理和辅助角公式将
| c |
| b |
| b |
| c |
解答:
.解:(I)∵B=C
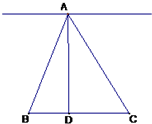
∴AD=2BD=2DC,
即tan
=
,
∴tanA=
=
,
∴sinA=
.
(II)由题意得:
bcsin?A=
a2,
∴
=sin?A,
则
+
=
=
=sin?A+2cos?A=
sin(A+θ),其中cosθ=
,
<θ<
,
易知B=C时,A最大,设为a,
由 (I)知,
<A<
,
又0<A<π,
∴A+θ∈(θ,θ+π)⊆(0,π),
∴当A+θ=
,即
sin(A+θ)取到最大值
,
当A→0时,
sin(A+θ)→2且
sin(A+θ)>2,
当A=π时,
sin(A+θ)=
×(
×
+
×
)=2,
∴
+
∈[2,
].

∴AD=2BD=2DC,
即tan
| A |
| 2 |
| 1 |
| 2 |
∴tanA=
2×
| ||
1-(
|
| 4 |
| 3 |
∴sinA=
| 4 |
| 5 |
(II)由题意得:
| 1 |
| 2 |
| 1 |
| 2 |
∴
| a2 |
| bc |
则
| c |
| b |
| b |
| c |
| b2+c2 |
| bc |
| a2+bccos?A |
| bc |
| 5 |
| 1 | ||
|
| π |
| 3 |
| π |
| 2 |
易知B=C时,A最大,设为a,
由 (I)知,
| π |
| 4 |
| π |
| 3 |
又0<A<π,
∴A+θ∈(θ,θ+π)⊆(0,π),
∴当A+θ=
| π |
| 2 |
| 5 |
| 5 |
当A→0时,
| 5 |
| 5 |
当A=π时,
| 5 |
| 5 |
| 4 |
| 5 |
| 1 | ||
|
| 3 |
| 5 |
| 2 | ||
|
∴
| c |
| b |
| b |
| c |
| 5 |
点评:本题主要考查正弦定理的应用,利用辅助角公式将函数进行化简是解决本题的关键,考查学生的计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“直线l与平面α内无数条直线都垂直”是“直线l与平面α垂直”的( )条件.
| A、必要非充分 |
| B、充分非必要 |
| C、充要 |
| D、既非充分又非必要 |
若sin(π+α)+sin(π-α)+sin(-α)=1,则sinα=( )
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
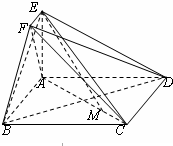 在如图所示的几何体中,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.
在如图所示的几何体中,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1.