题目内容
已知a,b是不相等的正常数,实数x,y∈(0,+∞).
(Ⅰ)求证:
+
≥
,并指出等号成立的条件;
(Ⅱ)求函数f(x)=
+
,x∈(0,
)的最小值,并指出此时x的值.
(Ⅰ)求证:
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
(Ⅱ)求函数f(x)=
| 2 |
| x |
| 1 |
| 1-2x |
| 1 |
| 2 |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:(Ⅰ)应用均值不等式,得:(
+
)(x+y)=a2+b2+
+
≥a2+b2+2
=a2+b2+2ab=(a+b)2,即可得出结论;
(Ⅱ)由(Ⅰ)知,f(x)=
+
≥
=9,从而可求函数的最小值.
| a2 |
| x |
| b2 |
| y |
| ya2 |
| x |
| xb2 |
| y |
|
(Ⅱ)由(Ⅰ)知,f(x)=
| 22 |
| 2x |
| 12 |
| 1-2x |
| (2+1)2 |
| 2x+(1-2x) |
解答:
(Ⅰ)证明:因为a,b是不相等的正常数,实数x,y∈(0,+∞),
所以应用均值不等式,得:(
+
)(x+y)=a2+b2+
+
≥a2+b2+2
=a2+b2+2ab=(a+b)2,即有
+
≥
,…(5分)
当且仅当
=
,即
=
时上式取等号; …(7分)
(Ⅱ)解:由(Ⅰ)知,f(x)=
+
≥
=9,…(10分)
当且仅当
=
,即x=
时上式取最小值,即f(x)min=9. …(12分)
所以应用均值不等式,得:(
| a2 |
| x |
| b2 |
| y |
| ya2 |
| x |
| xb2 |
| y |
|
=a2+b2+2ab=(a+b)2,即有
| a2 |
| x |
| b2 |
| y |
| (a+b)2 |
| x+y |
当且仅当
| ya2 |
| x |
| xb2 |
| y |
| a |
| x |
| b |
| y |
(Ⅱ)解:由(Ⅰ)知,f(x)=
| 22 |
| 2x |
| 12 |
| 1-2x |
| (2+1)2 |
| 2x+(1-2x) |
当且仅当
| 2 |
| 2x |
| 1 |
| 1-2x |
| 1 |
| 3 |
点评:本题考查运用均值不等式证明不等式与求函数的最值,考查学生分析解决问题的能力,正确证明不等式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
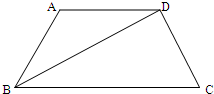 如图,在四边形ABCD中,
如图,在四边形ABCD中,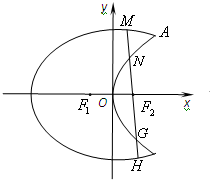 我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”.如图,“盾圆C”是由椭圆