题目内容
下列说法正确的有( )
(1)用反证法证明:“三角形的内角中至少有一个不大于60°”时的假设是“假设三角形的三个内角都不大于60°;
(2)分析法是从要证明的结论出发,逐步寻求使结论成立的充要条件;
(3)用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1),从k到k+1,左边需要增乘的代数式为2(2k+1);
(4)演绎推理是从特殊到一般的推理,其一般模式是三段论.
(1)用反证法证明:“三角形的内角中至少有一个不大于60°”时的假设是“假设三角形的三个内角都不大于60°;
(2)分析法是从要证明的结论出发,逐步寻求使结论成立的充要条件;
(3)用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1),从k到k+1,左边需要增乘的代数式为2(2k+1);
(4)演绎推理是从特殊到一般的推理,其一般模式是三段论.
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:综合题
分析:(1)根据反证法证明问题的一般步骤研究命题的否定,判定(1)是错误的;
(2)根据分析法的定义与证明问题的一般步骤,判定(2)是错误的;
(3)根据数学归纳法证明问题的步骤,结合题目,判定(3)是正确的;
(4)根据演绎推理的定义以及它的一般模式,判定(4)是错误的.
(2)根据分析法的定义与证明问题的一般步骤,判定(2)是错误的;
(3)根据数学归纳法证明问题的步骤,结合题目,判定(3)是正确的;
(4)根据演绎推理的定义以及它的一般模式,判定(4)是错误的.
解答:
解:(1)用反证法证明“三角形的内角中至少有一个不大于60°”时的假设是:
“假设三角形的三个内角都大于60°”,∴命题(1)错误;
(2)分析法是从要证明的结论出发,逐步寻求使结论成立的充分条件,∴命题(2)错误;
(3)用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)时,
从k到k+1,左边需要增乘的代数式为
=2(2k+1),∴命题(3)正确;
(4)演绎推理是由一般到特殊的推理,它的一般模式是“三段论”,
即大前提、小前提和结论,∴命题(4)错误.
综上,正确的命题是(3).
故选:B.
“假设三角形的三个内角都大于60°”,∴命题(1)错误;
(2)分析法是从要证明的结论出发,逐步寻求使结论成立的充分条件,∴命题(2)错误;
(3)用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)时,
从k到k+1,左边需要增乘的代数式为
| (2k+1)(2k+2) |
| k+1 |
(4)演绎推理是由一般到特殊的推理,它的一般模式是“三段论”,
即大前提、小前提和结论,∴命题(4)错误.
综上,正确的命题是(3).
故选:B.
点评:本题通过命题真假的判定,考查了反证法问题与命题的否定,分析法的概念,数学归纳法的应用,演绎推理的概念问题,是理解概念为主的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图所示的是某一几何体的三视图,则这个几何体是( )


| A、长方体 | B、圆锥 |
| C、圆柱 | D、正三棱锥 |
设随机变量是y的分布为:
则
≤y≤
的概率为( )
| y | -1 | 2 | 3 | ||||
| P |
|
m |
|
| 3 |
| 2 |
| 7 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
=(2,3)与
=(4,3y)共线,则y的值为( )
| a |
| b |
| A、2 | B、-6 | C、4 | D、-8 |
函数f(x)的导函数f′(x)的图象如图所示,则( )
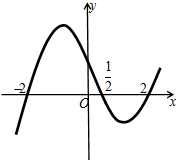

A、x=
| ||
| B、x=-2为f(x)的极大值点 | ||
| C、x=2为f(x)的极大值点 | ||
| D、x=0为f(x)的极小值点 |
定义在(0,
)上的函数f(x),f′(x)是它的导函数,且恒有f′(x)>f(x)•tanx成立.则( )
| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若x1,x2,x3,…x30这30个数据的平均数为
,方差为0.31,则x1,x2,x3,…x30,
的方差为( )
. |
| x |
. |
| x |
| A、0.4 | B、0.3 |
| C、0.04 | D、1 |
若等比数列{an}中a4=1,则a3+a4+a5的取值范围是( )
| A、(-∞,-1] |
| B、(-∞,0)∪(1,+∞) |
| C、[3,+∞) |
| D、(-∞,-1]∪[3,+∞) |