题目内容
函数y=sinx在点(
,
)处的切线方程是( )
| π |
| 3 |
| ||
| 2 |
A、x+2y-
| ||||
B、x+2y+
| ||||
C、x-2y-
| ||||
D、x-2y+
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:先求导函数,利用导函数在x=π处可知切线的斜率,利用点斜式,即可求得切线方程.
解答:
解:∵f(x)=sinx,
∴f′(x)=cosx
∴x=
时,f′(
)=cos
=
,
∴函数f(x)=sinx在点(
,
)处的切线方程为y-
=
(x-
),
即x-2y+
-
=0.
故选:D.
∴f′(x)=cosx
∴x=
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴函数f(x)=sinx在点(
| π |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 3 |
即x-2y+
| 3 |
| π |
| 3 |
故选:D.
点评:本题以正弦函数为载体,考查导数的几何意义,解题的关键是利用导数在切点的函数值为切线的斜率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
等差数列{an}中
<-1,它的前n项和Sn有最大值,则当Sn取得最小正值时,n=( )
| a11 |
| a10 |
| A、10 | B、11 | C、19 | D、20 |
函数f(x)的导函数f′(x)的图象如图所示,则( )
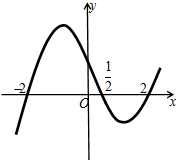

A、x=
| ||
| B、x=-2为f(x)的极大值点 | ||
| C、x=2为f(x)的极大值点 | ||
| D、x=0为f(x)的极小值点 |
如果生男孩和生女孩的概率相等,有一对夫妻生有3个小孩,已知这对夫妻的孩子有一个是女孩,那么这对夫妻有男孩的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若x1,x2,x3,…x30这30个数据的平均数为
,方差为0.31,则x1,x2,x3,…x30,
的方差为( )
. |
| x |
. |
| x |
| A、0.4 | B、0.3 |
| C、0.04 | D、1 |
函数f(x)=x3+ax2+bx+a2在x=1时有极值10,则a的值为( )
| A、-3或4 | B、4 |
| C、-3 | D、3或4 |
△ABC中,角A,B,C的对边边长分别为a=3,b=4,c=6,则bccosA+cacosB+abcosC=( )
| A、61 | ||
B、
| ||
C、
| ||
| D、122 |
函数f(x)=2x-xlnx的极值是( )
A、
| ||
B、
| ||
| C、e | ||
| D、e2 |
已知a>b>0,下列不等式成立的是( )
A、
| ||||
| B、ac>bc | ||||
| C、a2>b2 | ||||
D、
|