题目内容
直线kx-y-k+1=0(k∈R)过定点 .
考点:恒过定点的直线
专题:计算题,直线与圆
分析:将直线化简成点斜式的形式得:y-1=k(x-1),可得直线的斜率为k且经过定点(1,1),从而得到答案.
解答:
解:将直线kx-y-k+1=0化简为点斜式,可得y-1=k(x-1),
∴直线经过定点(1,1),且斜率为k.
即直线kx-y-k+1=0(k∈R)恒过定点(1,1).
故答案为:(1,1).
∴直线经过定点(1,1),且斜率为k.
即直线kx-y-k+1=0(k∈R)恒过定点(1,1).
故答案为:(1,1).
点评:本题给出含有参数k的直线方程,求直线经过的定点坐标.着重考查了直线的基本量与基本形式等知识,属于基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
等差数列{an}中
<-1,它的前n项和Sn有最大值,则当Sn取得最小正值时,n=( )
| a11 |
| a10 |
| A、10 | B、11 | C、19 | D、20 |
函数f(x)的导函数f′(x)的图象如图所示,则( )
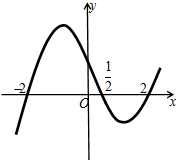

A、x=
| ||
| B、x=-2为f(x)的极大值点 | ||
| C、x=2为f(x)的极大值点 | ||
| D、x=0为f(x)的极小值点 |
 如图,函数y=f(x)的图象在点P(4,f(4))处的切线方程是y=-2x+9,则f(4)+f′(4)的值为
如图,函数y=f(x)的图象在点P(4,f(4))处的切线方程是y=-2x+9,则f(4)+f′(4)的值为