题目内容
双曲线
-
=1的焦点到渐近线的距离与顶点到渐近线的距离之比为（ ）
| x2 |
| 4 |
| y2 |
| 5 |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：过双曲线的顶点A、焦点F分别向其渐近线作垂线，垂足分别为B、C，根据比例线段的性质可知
=
=
=
，可得结论．
| |OF| |
| |OA| |
| |FC| |
| |AB| |
| c |
| a |
| 3 |
| 2 |
解答：
解：如图，过双曲线的顶点A、焦点F分别向其渐近线作垂线，
垂足分别为B、C，
则：
=
=
=
，
故选：A．
解：如图，过双曲线的顶点A、焦点F分别向其渐近线作垂线，垂足分别为B、C，
则：
| |OF| |
| |OA| |
| |FC| |
| |AB| |
| c |
| a |
| 3 |
| 2 |
故选：A．
点评：本题考查双曲线的简单性质；考查双曲线中几何量之间的关系，考查数形结合的能力，属于基础题．
练习册系列答案
相关题目
设随机变量是y的分布为：
则
≤y≤
的概率为（ ）
| y | -1 | 2 | 3 | ||||
| P |
|
m |
|
| 3 |
| 2 |
| 7 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）的导函数f′（x）的图象如图所示，则（ ）
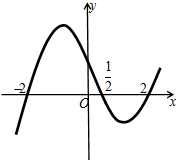
A、x=
| ||
| B、x=-2为f（x）的极大值点 | ||
| C、x=2为f（x）的极大值点 | ||
| D、x=0为f（x）的极小值点 |
定义在（0，
）上的函数f（x），f′（x）是它的导函数，且恒有f′（x）＞f（x）•tanx成立．则（ ）
| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
如果生男孩和生女孩的概率相等，有一对夫妻生有3个小孩，已知这对夫妻的孩子有一个是女孩，那么这对夫妻有男孩的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若x1，x2，x3，…x30这30个数据的平均数为
，方差为0.31，则x1，x2，x3，…x30，
的方差为（ ）
. |
| x |
. |
| x |
| A、0.4 | B、0.3 |
| C、0.04 | D、1 |
△ABC中，角A，B，C的对边边长分别为a=3，b=4，c=6，则bccosA+cacosB+abcosC=（ ）
| A、61 | ||
B、
| ||
C、
| ||
| D、122 |
已知函数f（x）=x2+bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2014的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|