题目内容
函数f(x)=cos(
-x)cosx是( )
| π |
| 2 |
| A、最小正周期为π的奇函数 | ||
B、最小正周期为
| ||
| C、最小正周期为π的偶函数 | ||
D、最小正周期为
|
考点:二倍角的正弦,运用诱导公式化简求值,三角函数的周期性及其求法,正弦函数的奇偶性
专题:三角函数的图像与性质
分析:根据三角函数的公式进行化简即可得到结论.
解答:
解:f(x)=cos(
-x)cosx=sinxcosx=
sin2x,
则函数的周期T=
=π,为奇函数,
故选:A
| π |
| 2 |
| 1 |
| 2 |
则函数的周期T=
| 2π |
| 2 |
故选:A
点评:本题主要考查三角函数的图象和性质,利用二倍角的正弦公式是解决本题的关键.

练习册系列答案
相关题目
函数f(x)的导函数f′(x)的图象如图所示,则( )
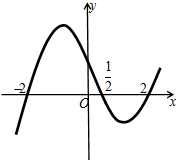

A、x=
| ||
| B、x=-2为f(x)的极大值点 | ||
| C、x=2为f(x)的极大值点 | ||
| D、x=0为f(x)的极小值点 |
△ABC中,角A,B,C的对边边长分别为a=3,b=4,c=6,则bccosA+cacosB+abcosC=( )
| A、61 | ||
B、
| ||
C、
| ||
| D、122 |
函数f(x)=2x-xlnx的极值是( )
A、
| ||
B、
| ||
| C、e | ||
| D、e2 |
若等比数列{an}中a4=1,则a3+a4+a5的取值范围是( )
| A、(-∞,-1] |
| B、(-∞,0)∪(1,+∞) |
| C、[3,+∞) |
| D、(-∞,-1]∪[3,+∞) |
过点P(0,1)与圆(x-1)2+y2=4相交的所有直线中,被圆截得的弦最长的直线方程是( )
| A、x+y-1=0 |
| B、x-y+1=0 |
| C、x=0 |
| D、y=1 |
已知函数f(x)=x2+bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2014的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a>b>0,下列不等式成立的是( )
A、
| ||||
| B、ac>bc | ||||
| C、a2>b2 | ||||
D、
|