题目内容
在△ABC中,若b=asinC,c=acosB,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
考点:三角形的形状判断
专题:解三角形
分析:由条件利用正弦定理可得 sinA=1,可得A=
.再由sinC=sinB,利用正弦定理可得c=b,可得△ABC的形状为等腰直角三角形.
| π |
| 2 |
解答:
解:在△ABC中,∵b=asinC,c=acosB,
故由正弦定理可得 sinB=sinAsinC,sinC=sinAsinB,
∴sinB=sinAsinAsinB,∴sinA=1,∴A=
.
∴sinC=sinAsinB 即 sinC=sinB,
∴由正弦定理可得c=b,故△ABC的形状为等腰直角三角形,
故选:C.
故由正弦定理可得 sinB=sinAsinC,sinC=sinAsinB,
∴sinB=sinAsinAsinB,∴sinA=1,∴A=
| π |
| 2 |
∴sinC=sinAsinB 即 sinC=sinB,
∴由正弦定理可得c=b,故△ABC的形状为等腰直角三角形,
故选:C.
点评:本题主要考查正弦定理的应用,判断三角型的形状,属于基础题.

练习册系列答案
相关题目
等差数列{an}中
<-1,它的前n项和Sn有最大值,则当Sn取得最小正值时,n=( )
| a11 |
| a10 |
| A、10 | B、11 | C、19 | D、20 |
如图所示的是某一几何体的三视图,则这个几何体是( )


| A、长方体 | B、圆锥 |
| C、圆柱 | D、正三棱锥 |
一个建筑队承包了两项工程,每项工程均有三项任务,由于工序的要求,第一项工程必须按照任务A、任务B、任务C的先后顺序进行,第二项工程必须按照任务D、任务E、任务F的先后顺序进行,建筑队每次只能完成一项任务,但第一项工程和第二项工程可以自由交替进行,若公司将两项工程做完,共有多少种安排方法( )
| A、12 | B、30 | C、20 | D、48 |
设随机变量是y的分布为:
则
≤y≤
的概率为( )
| y | -1 | 2 | 3 | ||||
| P |
|
m |
|
| 3 |
| 2 |
| 7 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)的导函数f′(x)的图象如图所示,则( )
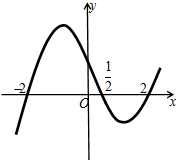

A、x=
| ||
| B、x=-2为f(x)的极大值点 | ||
| C、x=2为f(x)的极大值点 | ||
| D、x=0为f(x)的极小值点 |
△ABC中,角A,B,C的对边边长分别为a=3,b=4,c=6,则bccosA+cacosB+abcosC=( )
| A、61 | ||
B、
| ||
C、
| ||
| D、122 |