Question

5．已知二次函数的图象过点A（-2，0），B（2，0），C（0，-4）．
（1）试求出此函数的解析式；
（2）作出函数y=|f（x）|的大致图象，再判断其奇偶性、单调性（不需推理证明）

Answer 1

分析 （1）由题意，抛物线关于y轴对称，顶点坐标为C（0，-4），开口向上，设方程为y=ax²-4，（-2，0）代入可得a=1，即可求出函数的解析式；
（2）利用翻折变换，得到函数y=|f（x）|的大致图象，根据图象判断其奇偶性、单调性．

解答 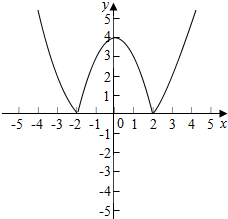解：（1）由题意，抛物线关于y轴对称，顶点坐标为C（0，-4），开口向上，
设方程为y=ax²-4，（-2，0）代入可得a=1，
∴函数的解析式为y=x²-4；
（2）函数y=|f（x）|的大致图象，如图所示．
函数是偶函数，单调增区间是（-2，0），（2，+∞）；单调减区间是（-∞，-2），（0，2）．

点评 本题考查二次函数的图象与性质，确定函数的解析式是关键．