题目内容
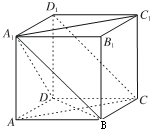已知正方体ABCD-A1B1C1D1．（1）求异面直线A1D与D1C所成的角；
（2）求证：面AA1C1C⊥面A1BD．
考点：平面与平面垂直的判定,异面直线及其所成的角
专题：空间位置关系与距离,空间角
分析：（1）由已知条件得A1BCD1是平行四边形，所以∠BA1D是异面直线A1D与D1C所成的角，由此能求出异面直线A1D与D1C所成的角．
（2）由正方形性质得BD⊥AC，由线面垂直的判定定理得BD⊥面AA1C1C，由此能证明面AA1C1C⊥面A1BD．
（2）由正方形性质得BD⊥AC，由线面垂直的判定定理得BD⊥面AA1C1C，由此能证明面AA1C1C⊥面A1BD．
解答：
（1）解：因为A1D1=BC且A1D1∥BC，
所以A1BCD1是平行四边形，则D1C∥A1B，
所以∠BA1D是异面直线A1D与D1C所成的角，
因为A1D=D1C=BD，所以∠BA1D=60°．
（2）证明：因为ABCD是正方形，所以BD⊥AC，
因为BD⊥CC1，AC∩CC1=C，所以BD⊥面AA1C1C，
因为BD?面A1BD，
所以面AA1C1C⊥面A1BD．
所以A1BCD1是平行四边形，则D1C∥A1B，
所以∠BA1D是异面直线A1D与D1C所成的角，
因为A1D=D1C=BD，所以∠BA1D=60°．
（2）证明：因为ABCD是正方形，所以BD⊥AC，
因为BD⊥CC1，AC∩CC1=C，所以BD⊥面AA1C1C，
因为BD?面A1BD，
所以面AA1C1C⊥面A1BD．
点评：本题考查异面直线所成角的大小的求法，考查面面垂直的证明，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
如图，已知正四棱锥S-ABCD的底面边长为2，高为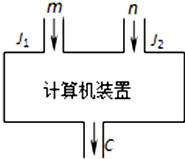
如图是一个计算机装置示意图，J1，J2是数据入口处，C是计算机结果的出口，计算过程是由J1，J2分别输入正整数m和n，经过计算后的结果由C输出．此种计算装置完成的计算满足以下三个性质：