题目内容
在△ABC中,若a=
,b=
,c=
;
(1)求角A的大小:
(2)求△ABC的面积及外接圆半径.
| 3 |
| 2 |
| ||||
| 2 |
(1)求角A的大小:
(2)求△ABC的面积及外接圆半径.
考点:余弦定理
专题:解三角形
分析:(1)利用余弦定理列出关系式,将a,b,c的值代入求出cosA的值,即可确定出A的度数;
(2)由b,c,sinA的值,利用三角形面积公式即可求出三角形ABC面积,利用正弦定理求出外接圆半径即可.
(2)由b,c,sinA的值,利用三角形面积公式即可求出三角形ABC面积,利用正弦定理求出外接圆半径即可.
解答:
解:(1)∵△ABC中,a=
,b=
,c=
,
∴cosA=
=
=
,
∵c>a>b,
∴A=60°;
(2)∵b=
,c=
,sinA=
,
∴S△ABC=
bcsinA=
×
×
×
=
;
由正弦定理
=2R得:R=
=
=1.
| 3 |
| 2 |
| ||||
| 2 |
∴cosA=
| b2+c2-a2 |
| 2bc |
2+
| ||||||||
2
|
| 1 |
| 2 |
∵c>a>b,
∴A=60°;
(2)∵b=
| 2 |
| ||||
| 2 |
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||||
| 2 |
| ||
| 2 |
3+
| ||
| 4 |
由正弦定理
| a |
| sinA |
| a |
| 2sinA |
| ||||
2×
|
点评:此题考查了正弦、余弦定理,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目

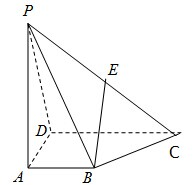 如图,在四棱锥P-ABCD中,AB∥DC,DC=2AB,E为PC的中点.
如图,在四棱锥P-ABCD中,AB∥DC,DC=2AB,E为PC的中点.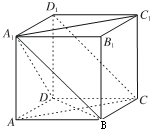 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.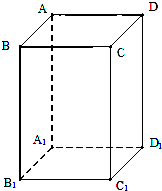 已知ABCD-A1B1C1D1是底面为正方形的直四棱柱,且A1B1=1,AA1=2,求:
已知ABCD-A1B1C1D1是底面为正方形的直四棱柱,且A1B1=1,AA1=2,求: