题目内容
如果椭圆的两焦点将长轴间的距离分成三等分，那么椭圆的离心率是 ．
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据题意分别表示出椭圆的焦距和长轴间的距离的三分之一，建立等式求得a和c的关系，则椭圆的离心率可得．
解答：
解：长轴长为2a，两焦点间的距离2c，
∵椭圆的两焦点将其长轴三等分，
∴2c=
•2a，即：3c=a，
∴e=
，
故答案为：
．
∵椭圆的两焦点将其长轴三等分，
∴2c=
| 1 |
| 3 |
∴e=
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题主要考查了椭圆的简单性质．求椭圆的离心率问题，通常有两种处理方法，一是求a，求c，再求比．二是列含a和c的齐次方程，再化含e的方程，解方程即可．
练习册系列答案
相关题目
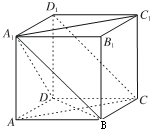已知正方体ABCD-A1B1C1D1．
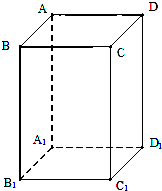已知ABCD-A1B1C1D1是底面为正方形的直四棱柱，且A1B1=1，AA1=2，求：