题目内容
已知sin(π+α)=2cos(π-α),计算:
(1)
(2)sin2α+sinαcosα-2cos2α
(1)
| 2sinα-cosα |
| sinα+2cosα |
(2)sin2α+sinαcosα-2cos2α
考点:诱导公式的作用,同角三角函数基本关系的运用,三角函数的化简求值
专题:三角函数的求值
分析:由于sin(π+α)=2cos(π-α),利用诱导公式和基本关系式可得tanα=2.
(1)利用基本关系式和“弦化切”即可得出;
(2)利用基本关系式和“弦化切”即可得出.
(1)利用基本关系式和“弦化切”即可得出;
(2)利用基本关系式和“弦化切”即可得出.
解答:
解:∵sin(π+α)=2cos(π-α),∴-sinα=-2cosα,∴tanα=2.
(1)原式=
=
=
.
(2)原式=
=
=
=
.
(1)原式=
| 2tanα-1 |
| tanα+2 |
| 2×2-1 |
| 2+2 |
| 3 |
| 4 |
(2)原式=
| sin2α+sinαcosα-2cos2α |
| sin2α+cos2α |
| tan2α+tanα-2 |
| tan2α+1 |
| 22+2-2 |
| 22+1 |
| 4 |
| 5 |
点评:本题考查了诱导公式和基本关系式、“弦化切”,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
在△ABC中,a、b、c分别是角A、B、C的对边,若a2+b2=2014c2,则
的值为( )
| 2tanA•tanB |
| tanC(tanA+tanB) |
| A、0 | B、1 |
| C、2013 | D、2014 |
不论m为何值,直线(m-1)x+(2m-1)y=m-5恒过定点( )
A、(1,-
| ||
| B、(-2,0) | ||
| C、(2,3) | ||
| D、(9,-4) |
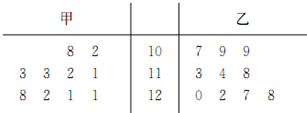 为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)
为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)