题目内容
将一个水平放置的正方形ABCD绕直线AB向上转动45°到ABC1D1,再将所得正方形ABC1D1绕直线BC1向上转动45°到A2BC1D2,则平面A2BC1D2与平面ABCD所成二面角的正弦值等于 .
考点:与二面角有关的立体几何综合题
专题:空间角
分析:利用三面角的第二余弦定理,建立等式,即可求解.
解答:
解:先来证明三面角的第二余弦定理:在三面角O-ABC中,设二面角B-OA-C为α,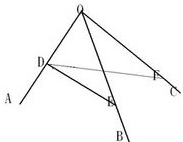 则有:cosα×sin∠AOB×sin∠AOC+cos∠AOB×cos∠AOC=cos∠BOC
则有:cosα×sin∠AOB×sin∠AOC+cos∠AOB×cos∠AOC=cos∠BOC
在OA上取一点D,过D作OD的垂线DE、DF分别交OB、OC于E与F.接着使用向量证明.考虑有向线段OD、OE、OF、DE、DF.易知:cosα=
,sin∠AOB=
,sin∠AOC=
,
cos∠AOB=
,cos∠AOC=
,cos∠BOC=
则实际是要证明:
×
×
+
×
=
利用
•
=
•
=
2可得出原式等价于
2+
•
=
•
∵
•
=(
+
)•(
+
)=
2+
•
+
•
+
•
,
•
=
•
=0,∴可证明原式.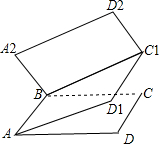
令∠ABC为α,α=90°,平面A₂BCD₂与平面ABCD所成角为A,二面角C₁-AB-D为D,二面角D₁-BC₁-E为B;
根据三面角的第二余弦定理有:cosA=-cosDcosB+sinDsinBcosα,所以cosA=-cos45°cos(180°-45°)+sin45°sin(180°-45°)cos90°,所以cosA=0.5,所以sinA=
.
故答案为:
.
 则有:cosα×sin∠AOB×sin∠AOC+cos∠AOB×cos∠AOC=cos∠BOC
则有:cosα×sin∠AOB×sin∠AOC+cos∠AOB×cos∠AOC=cos∠BOC在OA上取一点D,过D作OD的垂线DE、DF分别交OB、OC于E与F.接着使用向量证明.考虑有向线段OD、OE、OF、DE、DF.易知:cosα=
| ||||
|
|
| DE |
| OE |
| DF |
| OF |
cos∠AOB=
| ||||
|
|
| ||||
|
|
| ||||
|
|
则实际是要证明:
| ||||
|
|
| DE |
| OE |
| DF |
| OF |
| ||||
|
|
| ||||
|
|
| ||||
|
|
利用
| OD |
| OE |
| OD |
| OF |
| OD |
| OD |
| DE |
| DF |
| OE |
| OF |
∵
| OE |
| OF |
| OD |
| DE |
| OD |
| DF |
| OD |
| OD |
| DE |
| OD |
| DF |
| DE |
| DF |
| OD |
| DE |
| OD |
| DF |

令∠ABC为α,α=90°,平面A₂BCD₂与平面ABCD所成角为A,二面角C₁-AB-D为D,二面角D₁-BC₁-E为B;
根据三面角的第二余弦定理有:cosA=-cosDcosB+sinDsinBcosα,所以cosA=-cos45°cos(180°-45°)+sin45°sin(180°-45°)cos90°,所以cosA=0.5,所以sinA=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查面面角,考查第二余弦定理,考查学生分析解决问题的能力,难度较大.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
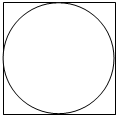 如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )
如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )A、1-
| ||
| B、π | ||
C、
| ||
D、1-
|