题目内容
已知x1,x2是关于x的一元二次方程x2+ax+2b=0的两个实数根,且x1∈(0,1),x2∈(1,2).则
的取值范围是 .
| b-2 |
| a-1 |
考点:简单线性规划,函数的零点
专题:不等式的解法及应用
分析:利用二次方程根的分布,建立不等式关系,利用线性规划以及
的几何意义求
的取值范围.
| b-2 |
| a-1 |
| b-2 |
| a-1 |
解答:
解;∵x1,x2是关于x的一元二次方程x2+ax+2b=0的两个实数根,
∴设函数f(x)=x2+ax+2b,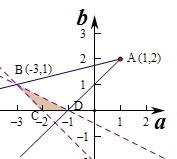
∵x1∈(0,1),x2∈(1,2).
∴
,即
,
作出不等式组对应的平面区域如图:
设z=
,则z的几何意义是区域内的点P(a,b)到定点A(1,2)两点之间斜率的取值范围,
由图象可知当P位于点B(-3,1)时,直线AB的斜率最小,此时k AB=
=
,
可知当P位于点D(-1,0)时,直线AD的斜率最大,此时kAD=
=1,
∴
<z<1,
则
的取值范围是(
,1).
故答案为:(
,1).
∴设函数f(x)=x2+ax+2b,

∵x1∈(0,1),x2∈(1,2).
∴
|
|
作出不等式组对应的平面区域如图:
设z=
| b-2 |
| a-1 |
由图象可知当P位于点B(-3,1)时,直线AB的斜率最小,此时k AB=
| 1-2 |
| -3-1 |
| 1 |
| 4 |
可知当P位于点D(-1,0)时,直线AD的斜率最大,此时kAD=
| 0-2 |
| -1-1 |
∴
| 1 |
| 4 |
则
| b-2 |
| a-1 |
| 1 |
| 4 |
故答案为:(
| 1 |
| 4 |
点评:本题主要考查二次方程根的分布,将二次方程转化为二次函数,然后利用线性规划求出目标函数的取值范围,注意目标函数的几何意义.

练习册系列答案
相关题目
 已知某几何体的三视图如图所示,其中俯视图中的曲线是一段半圆弧,则这个几何体的表面积是( )
已知某几何体的三视图如图所示,其中俯视图中的曲线是一段半圆弧,则这个几何体的表面积是( )| A、12-π | B、12+π |
| C、14-π | D、14+π |
x3+y3和x2-3xy-4y2的公因式为( )
| A、x+4y | B、x-4y |
| C、x-y | D、x+y |
全集U=R,集合A={x|2>2x-1≥1},集合B={x|y=ln(1-x)},则A∩(∁UB)=( )
| A、[1,2] |
| B、(1,2] |
| C、[1,2) |
| D、(-∞,2] |
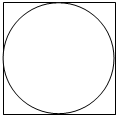 如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )
如图是一个边长为4的正方形及其内切圆,若随机向正方形内丢一粒豆子,假设豆子不落在线上,则豆子不落入圆内的概率是( )A、1-
| ||
| B、π | ||
C、
| ||
D、1-
|