题目内容
△ABC中，角A，B，C所对的边分别是a，b，c，若
=
（1）求角A；
（2）若f（x）=sin2（x+A）-cos2（x+A），求f（x）的单调递增区间．
| a-c |
| b-c |
| sinB |
| sinA+sinC |
（1）求角A；
（2）若f（x）=sin2（x+A）-cos2（x+A），求f（x）的单调递增区间．
考点：正弦定理,余弦定理
专题：三角函数的图像与性质,解三角形
分析：（1）通过正弦定理把已知等式中的角的正弦化成边，整理后利用余弦定理可求得cosA的值，进而求得A．
（2）利用二倍角公式对函数整理后，利用三角函数的性质求得函数的单调增区间．
（2）利用二倍角公式对函数整理后，利用三角函数的性质求得函数的单调增区间．
解答：
解：（1）由正弦定理得
=
，即a2=b2+c2-bc，
由余弦定理得cosA=
，
∴A=
；
（2）f(x)=sin2(x+
)-cos2(x+
)=-cos(2x+
)
当2kπ≤2x+
≤2kπ+π，即kπ-
≤x≤kπ+
，k∈Z时，函数单调增．
∴f（x）的单调递增区间为[kπ-
，kπ+
]，(k∈Z)
| a-c |
| b-c |
| b |
| a+c |
由余弦定理得cosA=
| 1 |
| 2 |
∴A=
| π |
| 3 |
（2）f(x)=sin2(x+
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
当2kπ≤2x+
| 2π |
| 3 |
| π |
| 3 |
| π |
| 6 |
∴f（x）的单调递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
点评：本题主要考查了正弦定理、余弦定理的综合运用，三角函数的图象与性质．注重了基础知识的综合运用．
练习册系列答案
相关题目
已知△ABC的顶点A（0，0），B（4，0），且AC边上的中线BD的长为3，则顶点C的轨迹方程是（ ）
| A、（x-8）2+y2=36（y≠0） |
| B、（x-4）2+y2=9（y≠0） |
| C、x2+y2=9（y≠0） |
| D、3x+4y-12=0（y≠0） |
若正实数x，y满足x+y=2，且
≥M恒成立，则M的最大值为（ ）
| 1 |
| xy |
| A、1 | B、2 | C、3 | D、4 |
函数y=sin2x-3sinx+2的最小值是（ ）
| A、2 | ||
| B、0 | ||
C、-
| ||
| D、6 |
已知α是第四象限的角，且sinα•cosα=-
，则sinα-cosα=（ ）
| 12 |
| 25 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
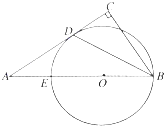如图，在Rt△ABC中，∠C=90°，E为AB上一点，以BE为直径作圆O与AC相切于点D．若AB：BC=2：1，CD=