题目内容
 如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1 则异面直线A1B与AC所成角的余弦值是( )
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1 则异面直线A1B与AC所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:由AC∥A1C1,知∠C1A1B是异面直线A1B与AC所成角,由此利用余弦定理能求出异面直线A1B与AC所成角的余弦值.
解答:
解:在直三棱柱ABC-A1B1C1中,
∵AC∥A1C1,∴∠C1A1B是异面直线A1B与AC所成角,
∵∠ACB=90°,AA1=2,AC=BC=1,
∴A1B=
=
,C1B=
=
,A1C1=1,
∴cos∠C1A1B=
=
.
∴异面直线A1B与AC所成角的余弦值是
.
故选:D.
∵AC∥A1C1,∴∠C1A1B是异面直线A1B与AC所成角,
∵∠ACB=90°,AA1=2,AC=BC=1,
∴A1B=
| 4+1+1 |
| 6 |
| 4+1 |
| 5 |
∴cos∠C1A1B=
| 6+1-5 | ||
2×1×
|
| ||
| 6 |
∴异面直线A1B与AC所成角的余弦值是
| ||
| 6 |
故选:D.
点评:本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
直线2x-my+1-3m=0,当m变动时,所有直线都通过定点( )
A、(-
| ||
B、(
| ||
C、(
| ||
D、(-
|
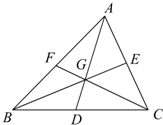 在△ABC中,AD,BE,CF分别是BC,CA,AB边上的中线,G是它们的交点,则下列等式中不正确的是( )
在△ABC中,AD,BE,CF分别是BC,CA,AB边上的中线,G是它们的交点,则下列等式中不正确的是( )A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
下列函数中,最小正周期是
的偶函数为( )
| π |
| 2 |
| A、y=tan2x | ||
B、y=cos(4x+
| ||
| C、y=2cos22x-1 | ||
| D、y=cos2x |
设A(-2,
),椭圆3x2+4y2=48的右焦点是F,点P在椭圆上移动,当|AP|+2|PF|取最小值时P点的坐标是( )
| 3 |
A、(0,2
| ||||
B、(0,-2
| ||||
C、(2
| ||||
D、(-2
|
双曲线两条渐近线的夹角为60°,该双曲线的离心率为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
函数f(x)=lgx+x-3的零点所在的区间是( )
| A、(1,2) |
| B、(3,4) |
| C、(2,3) |
| D、(0,1) |