题目内容
已知集合M={x|x=m+
n,m、n∈Z}
(1)若t∈Z,试判断t是否是集合M的元素;
(2)若x1、x2∈M,试判断x1+x2及x1x2是否属于集合M,如果属于,请给出证明;若不属于,请给出反例.
| 2 |
(1)若t∈Z,试判断t是否是集合M的元素;
(2)若x1、x2∈M,试判断x1+x2及x1x2是否属于集合M,如果属于,请给出证明;若不属于,请给出反例.
考点:元素与集合关系的判断
专题:函数的性质及应用
分析:(1)分当n≠0和当n=0两种情况,利用M中元素的形态分别讨论t与M的关系.
(2)若x1、x2∈M,则x1=a+
b,x2 =c+
d,且a、b、c、d∈Z,分别考查x1+x2 和x1•x2 的形态,从而确定它们与集合M的关系.
(2)若x1、x2∈M,则x1=a+
| 2 |
| 2 |
解答:
解:(1)∵M={x|x=m+
n,m、n∈Z},∴当n≠0时,x为无理数,若t∈Z,则t是不是集合M的元素.
当n=0时,x为整数,若t∈Z,则t是集合M的元素.
(2)若x1、x2∈M,则x1=a+
b,x2 =c+
d,且a、b、c、d∈Z,
∴x1+x2=a+c+(b+d)
,仍是m+
n,m、n∈Z的形式,故x1+x2 属于集合M.
根据 x1x2 =ac+2bd+(ad+bc)
,仍是m+
n,m、n∈Z的形式,故x1x2 属于集合M.
| 2 |
当n=0时,x为整数,若t∈Z,则t是集合M的元素.
(2)若x1、x2∈M,则x1=a+
| 2 |
| 2 |
∴x1+x2=a+c+(b+d)
| 2 |
| 2 |
根据 x1x2 =ac+2bd+(ad+bc)
| 2 |
| 2 |
点评:本题主要考查元素与集合的关系的判定,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
 如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1 则异面直线A1B与AC所成角的余弦值是( )
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1 则异面直线A1B与AC所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
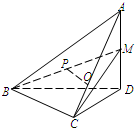 如图在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2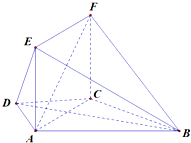 如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=
如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=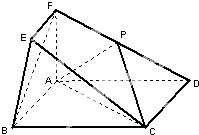 在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.
在如图所示的几何体中,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD=2,AB=AF=2EF=1,点P在棱DF上.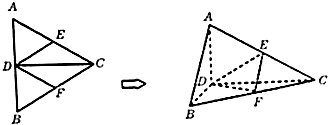
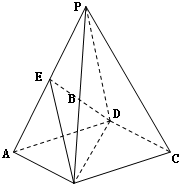 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证:
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证: