题目内容
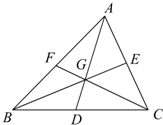在△ABC中，AD，BE，CF分别是BC，CA，AB边上的中线，G是它们的交点，则下列等式中不正确的是（ ）A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
考点：平行向量与共线向量
专题：平面向量及应用
分析：由三角形的重心定理和向量共线定理可得：
=
，
=-2
，
+
=
+
=
=
，
=
．即可判断出．
| BG |
| 2 |
| 3 |
| BE |
| CG |
| FG |
| 1 |
| 3 |
| DA |
| 2 |
| 3 |
| FC |
| DG |
| GC |
| DC |
| 1 |
| 2 |
| BC |
| DG |
| 1 |
| 2 |
| GA |
解答：
解：由三角形的重心定理可得：
=
，
=-2
，
+
=
+
=
=
，
=
．
可知：A，C，D都正确，B不正确．
故选：B．
| BG |
| 2 |
| 3 |
| BE |
| CG |
| FG |
| 1 |
| 3 |
| DA |
| 2 |
| 3 |
| FC |
| DG |
| GC |
| DC |
| 1 |
| 2 |
| BC |
| DG |
| 1 |
| 2 |
| GA |
可知：A，C，D都正确，B不正确．
故选：B．
点评：本题考查了三角形的重心定理和向量共线定理，属于中档题．
练习册系列答案
相关题目
正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=设sin2α=-sinα，α∈（
，π），则tan2α的值是（ ）
| π |
| 2 |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
设
=
，
=
，
=
，则
等于（ ）
| AB |
| a |
| AD |
| b |
| BC |
| c |
| DC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
函数f（x）的定义域为R，f（2）=4，对?x∈R，f′（x）＞3，则f（x）＞3x-2的解集是（ ）
| A、（-∞，+∞） |
| B、（2，+∞） |
| C、（-∞，2） |
| D、（-2，2） |
设集合U={1，2，3，4，5}，A={1，3，5}，B={2，3，5}，则A∪B=（ ）
| A、U | B、∅ |
| C、{3，5} | D、{1，2，3，5} |
如图在直三棱柱ABC-A1B1C1中，∠ACB=90°，AA1=2，AC=BC=1 则异面直线A1B与AC所成角的余弦值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知F1，F2分别是双曲线C：
-
=1的左、右两个焦点．若C上存在一点P，使得|
|•|
|=2a2，则C的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、（1，
| ||
B、[
| ||
C、（1，
| ||
D、[
|
如图，在梯形ABCD中，AD⊥CD，AD∥CD，AD=CD=