题目内容
函数f（x）=lgx+x-3的零点所在的区间是（ ）
| A、（1，2） |
| B、（3，4） |
| C、（2，3） |
| D、（0，1） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：函数零点左右两边函数值的符号相反，根据函数在一个区间上两个端点的函数值的符号确定是否存在零点．
解答：
解：f（2）=lg2+2-3=lg2-1＜0，
f（3）=lg3+3-3=lg3＞0，
零点定理知，
f（x）的零点在区间（2，3）上．
故选：C．
f（3）=lg3+3-3=lg3＞0，
零点定理知，
f（x）的零点在区间（2，3）上．
故选：C．
点评：本题考查函数的零点的判定定理，本题解题的关键是求出区间的两个端点的函数值，进行比较，本题是一个基础题．
练习册系列答案
相关题目
设sin2α=-sinα，α∈（
，π），则tan2α的值是（ ）
| π |
| 2 |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
如图在直三棱柱ABC-A1B1C1中，∠ACB=90°，AA1=2，AC=BC=1 则异面直线A1B与AC所成角的余弦值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知F1，F2分别是双曲线C：
-
=1的左、右两个焦点．若C上存在一点P，使得|
|•|
|=2a2，则C的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、（1，
| ||
B、[
| ||
C、（1，
| ||
D、[
|
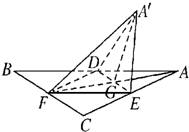如图，等边三角形ABC的中线AF与中位线DE相交于G，已知△A′ED是△ADE绕DE旋转过程中的一个图形，下列命题中，错误的是（ ）| A、动点A′在平面ABC上的射影在线段AF上 |
| B、恒有平面A′GF⊥平面ACDE |
| C、三棱锥′-EFD的体积有最大值 |
| D、异面直线A′E与BD不可能垂直 |
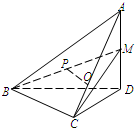如图在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2
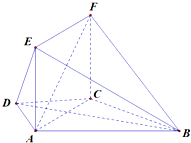如图，在梯形ABCD中，AD⊥CD，AD∥CD，AD=CD=
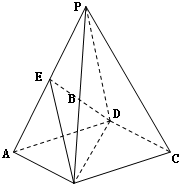如图，在四棱柱P-ABCD中，底面ABCD是矩形，E是棱PA的中点，PD⊥BC．求证：