题目内容
双曲线两条渐近线的夹角为60°，该双曲线的离心率为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：先由双曲线的两条渐近线的夹角为60°，得双曲线的两条渐近线的斜率±
或
，通过讨论分别计算离心率，即可得到结论．
| 3 |
| ||
| 3 |
解答：
解：∵双曲线的两条渐近线的夹角为60°，且渐近线关于x、y轴对称，
双曲线的两条渐近线中经过一象限的渐近线的倾斜角为30°或60°，斜率为
或
，
即
=
或
，
若
=
则b=
a，c=
=
=2a，
则离心率e=
=2，
若
=
，则b=
a，c=
=
=
a，
则离心率e=
=
综上所述，离心率为2或
，
故选：D
双曲线的两条渐近线中经过一象限的渐近线的倾斜角为30°或60°，斜率为
| 3 |
| ||
| 3 |
即
| b |
| a |
| 3 |
| ||
| 3 |
若
| b |
| a |
| 3 |
| 3 |
| a2+b2 |
| 4a2 |
则离心率e=
| c |
| a |
若
| b |
| a |
| ||
| 3 |
| ||
| 3 |
| a2+b2 |
a2+
|
2
| ||
| 3 |
则离心率e=
| c |
| a |
2
| ||
| 3 |
综上所述，离心率为2或
2
| ||
| 3 |
故选：D
点评：本题主要考查了双曲线的性质．当涉及两直线的夹角问题时要注意考虑两种方面．
练习册系列答案
相关题目
函数f（x）的定义域为R，f（2）=4，对?x∈R，f′（x）＞3，则f（x）＞3x-2的解集是（ ）
| A、（-∞，+∞） |
| B、（2，+∞） |
| C、（-∞，2） |
| D、（-2，2） |
如图在直三棱柱ABC-A1B1C1中，∠ACB=90°，AA1=2，AC=BC=1 则异面直线A1B与AC所成角的余弦值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某四面体的三视图如图所示，该四面体的表面积是（ ）
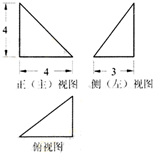
A、40+4
| ||
B、20+2
| ||
C、24+6
| ||
D、48+12
|
已知F1，F2分别是双曲线C：
-
=1的左、右两个焦点．若C上存在一点P，使得|
|•|
|=2a2，则C的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、（1，
| ||
B、[
| ||
C、（1，
| ||
D、[
|
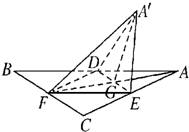如图，等边三角形ABC的中线AF与中位线DE相交于G，已知△A′ED是△ADE绕DE旋转过程中的一个图形，下列命题中，错误的是（ ）| A、动点A′在平面ABC上的射影在线段AF上 |
| B、恒有平面A′GF⊥平面ACDE |
| C、三棱锥′-EFD的体积有最大值 |
| D、异面直线A′E与BD不可能垂直 |
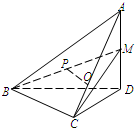如图在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2