题目内容
函数y=2sin(
-x)的一个单调增区间是( )
| π |
| 4 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
考点:正弦函数的单调性
专题:三角函数的图像与性质
分析:先把已知函数利用诱导公式化简可得y=2sin(
-x)=2sin[π-(
-x)]=2sin(x+
),要求函数的单调增区间,转化为求函数g(x)=sin(x+
)的单调减区间.
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
解答:
解:∵y=2sin(
-x)=2sin[π-(
-x)]=2sin(x+
),
令g(x)=sin(x+
),
由:-
+2kπ≤x+
≤
+2kπ,k∈Z可得:-
+2kπ≤x≤-
+2kπ,k∈Z,
当k=0时,[-
,-
]为函数y=2sin(
-x)的一个单调增区间.
故选:C
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
令g(x)=sin(x+
| 3π |
| 4 |
由:-
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
| 5π |
| 4 |
| π |
| 4 |
当k=0时,[-
| 5π |
| 4 |
| π |
| 4 |
| π |
| 4 |
故选:C
点评:本题主要考查了三角函数y=Asin(ωx+θ)的单调区间,求解的基本方法是利用诱导公式把函数进行化简,使得x的系数ω化为正,然后结合正弦函数的单调区间求解.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
P是椭圆
+
=1上一点,F1,F2分别为左、右焦点,△PF1F2的内切圆的半径为1,则|
+
|的值为( )
| x2 |
| 25 |
| y2 |
| 9 |
| PF1 |
| PF2 |
| A、8 | ||||
B、4
| ||||
| C、4 | ||||
D、
|
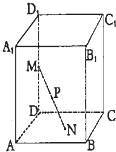 已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )
已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
若正实数x,y满足x+y+
+
=5,则x+y的最大值是( )
| 1 |
| x |
| 1 |
| y |
| A、2 | B、3 | C、4 | D、5 |
有穷数列1,23,26,29,…,23n+6的项数是( )
| A、3n+7 | B、3n+6 |
| C、n+3 | D、n+2 |
已知f(x)=x3+x2f′(1),则f′(2)=( )
| A、0 | B、1 | C、2 | D、3 |