题目内容
若正实数x,y满足x+y+
+
=5,则x+y的最大值是( )
| 1 |
| x |
| 1 |
| y |
| A、2 | B、3 | C、4 | D、5 |
考点:基本不等式
专题:不等式的解法及应用
分析:由已知的等式结合基本不等式得到(x+y)2-5(x+y)+4≤0,求解一元二次不等式得答案.
解答:
解:由x+y+
+
=5,得(x+y)+
=5.
即5=(x+y)+
≥(x+y)+
,
(x+y)2-5(x+y)+4≤0.
解得:1≤x+y≤4.
∴x+y的最大值是4.
故选:C.
| 1 |
| x |
| 1 |
| y |
| x+y |
| xy |
即5=(x+y)+
| x+y |
| xy |
| 4 |
| x+y |
(x+y)2-5(x+y)+4≤0.
解得:1≤x+y≤4.
∴x+y的最大值是4.
故选:C.
点评:本题考查了基本不等式,考查了数学转化思想方法,是基础题.

练习册系列答案
相关题目
函数y=2sin(
-x)的一个单调增区间是( )
| π |
| 4 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
如图,△AOB是一个水平放置的平面图形的直观图,则其平面图形的面积为( )
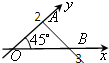

| A、3 | ||||
| B、6 | ||||
C、3
| ||||
D、
|
函数y=
+
是( )
| 1-x2 |
| 2 |
| 1+|x| |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
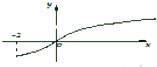 已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为
已知f(x)的定义域为[-2,+∞),部分对应值如下表,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图,若f(x)<1,则x的范围为