题目内容
将边长为1的正方形ABCD沿对角线AC折起,使得平面ADC⊥平面ABC,在折起后形成的三棱锥D-ABC中,给出下列三个命题:
①面DBC是等边三角形;
②AC⊥BD;
③三棱锥D-ABC的体积是
.
其中正确命题的序号是 .(写出所有正确命题的序号)
①面DBC是等边三角形;
②AC⊥BD;
③三棱锥D-ABC的体积是
| ||
| 6 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:先作出图来,①根据图可知BD=
DO=1,再由BC=DC=1,可知面DBC是等边三角形.
②由AC⊥DO,AC⊥BO,可得AC⊥平面DOB,从而有AC⊥BD.
③三棱锥D-ABC的体积=
S△ABC•OD=
•
•1•1•
=
.
| 2 |
②由AC⊥DO,AC⊥BO,可得AC⊥平面DOB,从而有AC⊥BD.
③三棱锥D-ABC的体积=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
解答:
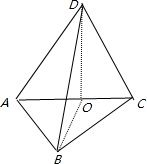 解:如图所示:BD=
解:如图所示:BD=
DO=
×
=1
又BC=DC=1
∴面DBC是等边三角形,即①正确;
∵AC⊥DO,AC⊥BO
∴AC⊥平面DOB
∴AC⊥BD,即②正确;
三棱锥D-ABC的体积=
S△ABC•OD=
•
•1•1•
=
,
③不正确.
故答案为:①②.
 解:如图所示:BD=
解:如图所示:BD=| 2 |
| 2 |
| ||
| 2 |
又BC=DC=1
∴面DBC是等边三角形,即①正确;
∵AC⊥DO,AC⊥BO
∴AC⊥平面DOB
∴AC⊥BD,即②正确;
三棱锥D-ABC的体积=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 12 |
③不正确.
故答案为:①②.
点评:本题主要考查折叠问题,要注意折叠前后的改变的量和位置,不变的量和位置,属中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
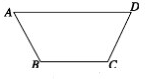 设计一个水渠,其横截面为等腰梯形(如图所示),要求满足条件AB+BC+CD=a(常数),∠ABC=120°,写出横截面的面积y与腰长x的关系式,并求它的定义域和值.
设计一个水渠,其横截面为等腰梯形(如图所示),要求满足条件AB+BC+CD=a(常数),∠ABC=120°,写出横截面的面积y与腰长x的关系式,并求它的定义域和值.