Question

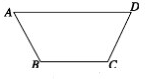设计一个水渠，其横截面为等腰梯形（如图所示），要求满足条件AB+BC+CD=a（常数），∠ABC=120°，写出横截面的面积y与腰长x的关系式，并求它的定义域和值．

Answer 1

考点：函数解析式的求解及常用方法,函数的定义域及其求法

专题：应用题,函数的性质及应用

分析：画出图形，结合图形，求出高和上底、下底的长，写出横截面的面积y的解析式，求出它的定义域和值域．

解答： 解：如图所示，
∵腰长AB=x，∠ABC=120°，∴高h=xcos30°=

3

2

x；
∴上底BC=a-2x（0＜x＜

a

2

），
下底AD=BC+2•xsin30°=（a-2x）+2x•

1

2

=a-x；
∴横截面的面积为
y=

1

2

[（a-2x）+（a-x）]•

3

2

x=-

3 3

4

x²+

3

2

ax（0＜x＜

a

2

）；
∵0＜x＜

a

2

，y=

3

2

（-

3

2

x²+ax），
∴当x=

a

3

时，y取得最大值y_max=

3

12

a²；
∴函数y的值域是（0，

3

12

a²]，定义域是（0，

a

2

）．

点评：本题考查了求函数的解析式、定义域和值域的问题，解题时应认真分析题意，建立函数的解析式，求出函数的定义域和值域，是综合题．