题目内容
设函数f(x)为奇函数,当x∈[-2,0]时,f(x)=
x3+x2-2ax(a为实数)
(1)若f(x)在x=-1处有极值,求a的值;
(2)求x∈(0,2]时,f(x)的解析式;
(3)若f(x)在[
,2]上为增函数,求a的取值范围.
| 1 |
| 3 |
(1)若f(x)在x=-1处有极值,求a的值;
(2)求x∈(0,2]时,f(x)的解析式;
(3)若f(x)在[
| 3 |
| 2 |
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(1)求导数,利用f(x)在x=-1处有极值,可得f′(-1)=1-2-2a=0,即可求a的值;
(2)设x∈(0,2],则-x∈[-2,0),利用条件,即可求x∈(0,2]时,f(x)的解析式;
(3)若f(x)在[
,2]上为增函数,则f′(x)=x2+2x-2a≥0在[
,2]上恒成立,分离参数求最小值,即可求a的取值范围.
(2)设x∈(0,2],则-x∈[-2,0),利用条件,即可求x∈(0,2]时,f(x)的解析式;
(3)若f(x)在[
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)∵f(x)=
x3+x2-2ax,
∴f′(x)=x2+2x-2a,
∵f(x)在x=-1处有极值,
∴f′(-1)=1-2-2a=0,
∴a=-
;
(2)设x∈(0,2],则-x∈[-2,0),
∴f(-x)=-
x3+x2+2ax,
∵函数f(x)为奇函数,
∴f(x)=-f(-x)=
x3-x2-2ax;
(3)∵f(x)在[
,2]上为增函数,
∴f′(x)=x2+2x-2a≥0在[
,2]上恒成立,
∴2a≤x2+2x在[
,2]上恒成立,
∴2a≤
+3,
∴a≤
.
| 1 |
| 3 |
∴f′(x)=x2+2x-2a,
∵f(x)在x=-1处有极值,
∴f′(-1)=1-2-2a=0,
∴a=-
| 1 |
| 2 |
(2)设x∈(0,2],则-x∈[-2,0),
∴f(-x)=-
| 1 |
| 3 |
∵函数f(x)为奇函数,
∴f(x)=-f(-x)=
| 1 |
| 3 |
(3)∵f(x)在[
| 3 |
| 2 |
∴f′(x)=x2+2x-2a≥0在[
| 3 |
| 2 |
∴2a≤x2+2x在[
| 3 |
| 2 |
∴2a≤
| 9 |
| 4 |
∴a≤
| 21 |
| 8 |
点评:了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号).会用导数判断函数单调性、求单调区间与极值.

练习册系列答案
相关题目
当输入x=-4时,如图的程序运行的结果是( )


| A、7 | B、8 | C、9 | D、15 |
已知某生产厂家的年利润y(单位:万元)与年产量x(单位:万件)的函数关系式为y=-
x3+49x-234则使该生产厂家获得最大年利润的年产量为( )
| 1 |
| 3 |
| A、13万件 | B、11万件 |
| C、9万件 | D、7万件 |
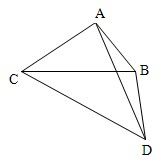 在三棱锥A-BCD中,平面ACB⊥平面BCD.在等腰直角三角形ABC中,AC=AB,AC=6,在Rt△BCD中,BC⊥BD,∠BCD=30°
在三棱锥A-BCD中,平面ACB⊥平面BCD.在等腰直角三角形ABC中,AC=AB,AC=6,在Rt△BCD中,BC⊥BD,∠BCD=30°