题目内容
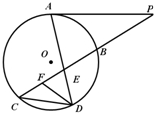 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=考点:弦切角
专题:立体几何
分析:利用△DEF∽△CED与已知可得EC的长,进而得到BE,利用相交弦定理可得AE•ED=EB•CE,得到AE.再利用AP∥CD,可得△AEP∽△FED,得到PE,进而得到PB,再利用切割线定理可得PA2=PB•PC即可得出.
解答:
解:在△DEF和△CED中,∵∠EDF=∠C,∠DEF公用,∴△DEF∽△CED,∴
=
,
∵DE=3,EF=2,∴EC=
=
=
.
∵CE:BE=3:2,∴BE=3.
由相交弦定理可得AE•ED=EB•CE,∴AE=
=
.
∵AP∥CD,∴∠P=∠C,
∴∠P=∠EDF.
∴△AEP∽△FED,∴
=
,
∴PE=
=
=
.
∴PB=PE-EB=
-3=
.
∵PA与⊙O相切,∴PA2=PB•PC=
×(
+3+
)=
.
∴PA=
.
故答案为:
.
| DE |
| EC |
| FE |
| ED |
∵DE=3,EF=2,∴EC=
| DE2 |
| FE |
| 32 |
| 2 |
| 9 |
| 2 |
∵CE:BE=3:2,∴BE=3.
由相交弦定理可得AE•ED=EB•CE,∴AE=
3×
| ||
| 3 |
| 9 |
| 2 |
∵AP∥CD,∴∠P=∠C,
∴∠P=∠EDF.
∴△AEP∽△FED,∴
| AE |
| EF |
| PE |
| ED |
∴PE=
| AE•ED |
| EF |
| ||
| 2 |
| 27 |
| 4 |
∴PB=PE-EB=
| 27 |
| 4 |
| 15 |
| 4 |
∵PA与⊙O相切,∴PA2=PB•PC=
| 15 |
| 4 |
| 15 |
| 4 |
| 9 |
| 2 |
| 15×45 |
| 4×4 |
∴PA=
15
| ||
| 4 |
故答案为:
15
| ||
| 4 |
点评:本题综合考查了相似三角形的判定与性质、相交弦定理、切割线定理、平行线的性质等基础知识与基本技能方法,考查了分析问题和解决问题的能力,考查了推理能力和计算能力,属于难题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
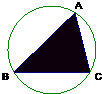 如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )
如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={x|(
)x<1},B={x|x2-3x-4>0},则A∩B等于( )
| 1 |
| 2 |
| A、{x|x>0} |
| B、{x|x<-1或x>0} |
| C、{x|x>4} |
| D、{x|-1≤x≤4} |
已知函数f(x)是定义在R上的偶函数,它在[0,+∞)上是减函数.则下列各式一定成立的是( )
| A、f(0)<f(6) |
| B、f(-3)>f(2) |
| C、f(-1)>f(3) |
| D、f(-2)<f(-3) |
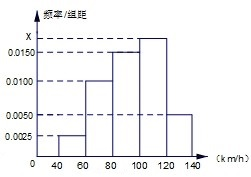 根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有
根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有