题目内容
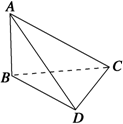如图，在四面体ABCD中，AB=1，AD=2| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：二面角的平面角及求法
专题：空间角
分析：
与
的夹角是θ二面角A-BC-D的平面角=π-θ，由
2=（
+
+
）2，能求出二面角A-BC-D的平面角．
| AB |
| CD |
| AD |
| AB |
| BC |
| CD |
解答：
解：设
与
的夹角是θ
二面角A-BC-D的平面角=π-θ，
∵在四面体ABCD中，AB=1，AD=2
，BC=3，CD=2，∠ABC=∠DCB=
，
=
+
+
，
∴
2=（
+
+
）2
=
2+
2+
2+2|
|•|
|•cos∠ABC+2|
|•|
|•cosθ+2|
|•|
|•cos（180°-∠BCD）
∴12=1+9+4+0+2×1×2×cosθ+0
解得cosθ=-
，∴θ=
°
∴二面角A-BC-D的平面角为π-
=
．
故选：B．
| AB |
| CD |
二面角A-BC-D的平面角=π-θ，
∵在四面体ABCD中，AB=1，AD=2
| 3 |
| π |
| 2 |
| AD |
| AB |
| BC |
| CD |
∴
| AD |
| AB |
| BC |
| CD |
=
| AB |
| BC |
| CD |
| AB |
| BC |
| AB |
| CD |
| BC |
| CD |
∴12=1+9+4+0+2×1×2×cosθ+0
解得cosθ=-
| 1 |
| 2 |
| 2π |
| 3 |
∴二面角A-BC-D的平面角为π-
| 2π |
| 3 |
| π |
| 3 |
故选：B．
点评：本题考查二面角的求法，是中档题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
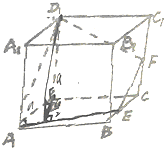已知E、F分别为正方体ABCD-A1B1C1D1的棱BC，CC1的中点，设α为二面角D-AE-D1的平面角，求sinα=（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知sinα+cosα=
，则sinα•cosα的值为（ ）
| 17 |
| 13 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
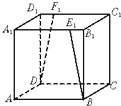如图，正方体ABCD-A1B1C1D1中，E1、F1分别是A1B1、C1D1上的点，并且4B1E1=4D1F1=A1B1，则BE1与DF1所成角的余弦值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知A、B、M三点不共线，对于平面ABM外任意一点O，若
+
=3
-
，则点P与A、B、M（ ）
| OB |
| OM |
| OP |
| OA |
| A、共面 | B、共线 |
| C、不共面 | D、不确定 |
如图所示，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AB=2，BC=1，