题目内容
已知函数f(x)=x3+ax2+bx+c(a,b,c∈R)在x=-
与x=1时都取得极值.
(1)求a,b的值与函数f(x)的单调区间;
(2)若函数g(x)=f(x)-2c在区间[-1,2]内恰有两个零点,求c的取值范围.
| 2 |
| 3 |
(1)求a,b的值与函数f(x)的单调区间;
(2)若函数g(x)=f(x)-2c在区间[-1,2]内恰有两个零点,求c的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(1)求导f′(x)=3x2+2ax+b,再由题意可得
,从而求出a,b;再求单调区间;
(2)由(1)列表,从而可得-
+c<2c<
+c或2c=
+c,从而解得.
|
(2)由(1)列表,从而可得-
| 3 |
| 2 |
| 1 |
| 2 |
| 22 |
| 27 |
解答:
解:(1)f′(x)=3x2+2ax+b,
∵x=-
与x=1时都取得极值,
∴
,
解得,a=-
,b=-2;
此时f′(x)=3x2-x-2=(3x+2)(x-1),
经检验,-
与1是函数的极值点;
令f′(x)>0,则x<-
或x>1;
令f′(x)<0,则-
<x<1;
∴单调增区间为(-∞,-
),(1,+∞),单调减区间为(-
,1).
(2)由(1)得
∵函数g(x)=f(x)-2c在区间[-1,2]内恰有两个零点,
∴-
+c<2c<
+c或2c=
+c,
即-
<c<
或c=
;
∴c的取值范围为-
<c<
或c=
.
∵x=-
| 2 |
| 3 |
∴
|
解得,a=-
| 1 |
| 2 |
此时f′(x)=3x2-x-2=(3x+2)(x-1),
经检验,-
| 2 |
| 3 |
令f′(x)>0,则x<-
| 2 |
| 3 |
令f′(x)<0,则-
| 2 |
| 3 |
∴单调增区间为(-∞,-
| 2 |
| 3 |
| 2 |
| 3 |
(2)由(1)得
| x | -1 | (-1,-
| -
| (-
| 1 | (1,2) | 2 | ||||||
f′(x) | 正 | 0 | 负 | 0 | 正 | ||||||||
| f(x) |
| 单调递增 |
| 单调递减 | -
| 单调递增 | 2+c |
∴-
| 3 |
| 2 |
| 1 |
| 2 |
| 22 |
| 27 |
即-
| 3 |
| 2 |
| 1 |
| 2 |
| 22 |
| 27 |
∴c的取值范围为-
| 3 |
| 2 |
| 1 |
| 2 |
| 22 |
| 27 |
点评:本题考查了导数的综合应用及函数的零点与函数图象的关系应用,属于中档题.

练习册系列答案
相关题目
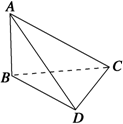 如图,在四面体ABCD中,AB=1,AD=2
如图,在四面体ABCD中,AB=1,AD=2| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
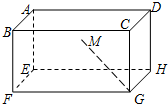 如图所示,在长方体ABCD-EFGH中,AD=2,AB=AE=1,M为矩形AEHD内的一点,如果∠MGF=∠MGH,MG和平面EFG所成角的正切值为
如图所示,在长方体ABCD-EFGH中,AD=2,AB=AE=1,M为矩形AEHD内的一点,如果∠MGF=∠MGH,MG和平面EFG所成角的正切值为