题目内容
已知x∈R,奇函数f(x)=x3+ax2+bx+c在[1,+∞)上单调,则a,b,c应满足的条件是 .
考点:函数的单调性与导数的关系,函数奇偶性的性质,奇偶性与单调性的综合
专题:导数的综合应用
分析:根据函数的奇偶性确定a=c=0,然后利用函数单调性和导数之间的关系即可得到结论.
解答:
解:∵f(x)=x3+ax2+bx+c是奇函数,
∴f(0)=c=0,
f(-x)=-f(x),
即-x3+ax2-bx=-x3-ax2-bx,
则a=-a,解得a=0,
则f(x)=x3+bx,
函数的导数f′(x)=2x2+b,
若b≥0,则f′(x)≥0恒成立,此时满足在[1,+∞)上单调递增,
若b<0,
由f′(x)=2x2+b≥0,解得x≥
或x≤-
,
即在[
,+∞)上单调递增,
若f(x)=x3+ax2+bx+c在[1,+∞)上单调,
则满足
≤1,
解得-2≤b<0,
综上b≥-2,
故满足的条件是a=c=0,b≥-2,
故答案为:a=c=0,b≥-2
∴f(0)=c=0,
f(-x)=-f(x),
即-x3+ax2-bx=-x3-ax2-bx,
则a=-a,解得a=0,
则f(x)=x3+bx,
函数的导数f′(x)=2x2+b,
若b≥0,则f′(x)≥0恒成立,此时满足在[1,+∞)上单调递增,
若b<0,
由f′(x)=2x2+b≥0,解得x≥
|
|
即在[
|
若f(x)=x3+ax2+bx+c在[1,+∞)上单调,
则满足
|
解得-2≤b<0,
综上b≥-2,
故满足的条件是a=c=0,b≥-2,
故答案为:a=c=0,b≥-2
点评:本题主要考查函数奇偶性和单调性的应用,根据奇函数的定义以及函数的导数研究函数的单调性是解决本题的关键.

练习册系列答案
相关题目
函数f(x)=lg(x2-ax+3)的定义域为R,则实数a的取值范围是( )
A、[-2
| ||||
B、(-2
| ||||
C、(-∞,-2
| ||||
D、(-∞,-2
|
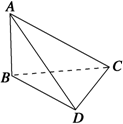 如图,在四面体ABCD中,AB=1,AD=2
如图,在四面体ABCD中,AB=1,AD=2| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|