题目内容
5.已知命题p:?m∈[-1,1],不等式a2-5a+7≥m+2恒成立;命题q:x2+ax=2=0有两个不同的实数根,若p∨q为真,且p∧q为假,求实数a的取值范围.分析 先求出当p真、q真时,a的取值范围,由p、q一真一假列式计算即可,
解答 解:命题p真:?m∈[-1,1],不等式a2-5a+7≥m+2恒成立⇒a2-5a+7≥(m+2)max=3⇒a≤1或a≥4;
命题q真:x2+ax=2=0有两个不同的实数根⇒△=a2-8>0⇒a<-$2\sqrt{2}$或a$>2\sqrt{2}$;
若p∨q为真,且p∧q为假,则p、q一真一假,
当p真q假时,$\left\{\begin{array}{l}{a≤1或a≥4}\\{-2\sqrt{2}≤a≤2\sqrt{2}}\end{array}\right.$⇒-2$\sqrt{2}$≤a≤1
当p假q真时,$\left\{\begin{array}{l}{1<a<4}\\{a<-2\sqrt{2}或a>2\sqrt{2}}\end{array}\right.$⇒2$\sqrt{2}$<a<4
∴实数a的取值范围为:⇒-2$\sqrt{2}$≤a≤1或2$\sqrt{2}$<a<4.
点评 本题考查了复合命题的真假的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.设F1,F2是椭圆C1:$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}$=1(a1>b1>0)与双曲线C2:$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}$=1(a2>0,b2>0)的公共焦点,曲线C1,C2在第一象限内交于点M,∠F1MF2=90°,若椭圆C1的离心率e1∈[$\frac{{\sqrt{6}}}{3}$,1),则双曲线C2的离心率e2的范围是( )
| A. | $({1,\sqrt{3}}]$ | B. | $({1,\sqrt{2}}]$ | C. | $[{\sqrt{3},+∞})$ | D. | $[{\sqrt{2},+∞})$ |
13.若命题:“?x∈R,使得ax2+(a-3)x+1<0”为假命题.则实数a的范围为( )
| A. | 0<a≤1或a≥9 | B. | a≤1或a≥9 | C. | 1≤a≤9 | D. | a≥9 |
10.已知cos(θ+$\frac{5π}{12}$)=-$\frac{\sqrt{2}}{2}$,且θ为锐角,则cos($\frac{π}{4}$-θ)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
14.已知数列{an}为等差数列,且a1+a7+a13=4π,则cos(a2+a12)=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
15.已知$a={5^{{{log}_3}3.4}},b={5^{{{log}_4}3.6}},c={(\frac{1}{5})^{{{log}_3}0.3}}$,则( )
| A. | c>a>b | B. | b>a>c | C. | b>a>c | D. | a>c>b |
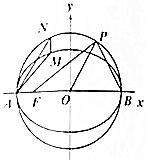 已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.
已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.