题目内容
15.已知$a={5^{{{log}_3}3.4}},b={5^{{{log}_4}3.6}},c={(\frac{1}{5})^{{{log}_3}0.3}}$,则( )| A. | c>a>b | B. | b>a>c | C. | b>a>c | D. | a>c>b |
分析 利用对数函数、指数函数的单调性求解.
解答 解:∵$a={5^{{{log}_3}3.4}},b={5^{{{log}_4}3.6}},c={(\frac{1}{5})^{{{log}_3}0.3}}$=${5}^{lo{g}_{3}\frac{10}{3}}$,
0<log41<log43.6<log44=1,
$lo{g}_{3}3.4>lo{g}_{3}\frac{10}{3}>lo{g}_{3}3=1$,
y=5x是增函数,
∴a>c>b.
故选:D.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意对数函数、指数函数的单调性的合理运用.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
6.已知集合A={x|log${\;}_{\frac{1}{2}}$x>-1},B=|x|2x>$\sqrt{2}$|,则A∪B=( )
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,+∞) | C. | (0,+∞) | D. | (0,2) |
4.已知p:幂函数y=(m2-m-1)xm在(0,+∞)上单调递增;q:|m-2|<1,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不要条件 |
5.某商场计划在今年同时出售智能手机和变频空调,两种市场销售情况很好(有多少就能卖多少)的新产品,
一次该商场要根据实际情况(如资金、劳动力(工资)等)准备好月资金工艺量,以使每月的总利润达到最大,通过一个月的市场调查,得到销售这两种产品的有关数据如表:
怎样确定这两种产品的月供应量,才能使每月的总利润最大,总利润的最大值是多少百元?
一次该商场要根据实际情况(如资金、劳动力(工资)等)准备好月资金工艺量,以使每月的总利润达到最大,通过一个月的市场调查,得到销售这两种产品的有关数据如表:
| 资金 | 产品所需资金(百元/台) | 月资金供应量(百元) | |
| 手机 | 空调 | ||
| 成本 | 40 | 30 | 600 |
| 劳动力(工资) | 2 | 5 | 58 |
| 利润 | 11 | 10 | |
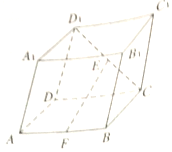 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为矩形,平面CDD1C1⊥平面ABCD,E,F分别是CD,AB的中点,求证:
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为矩形,平面CDD1C1⊥平面ABCD,E,F分别是CD,AB的中点,求证: