题目内容
10.已知cos(θ+$\frac{5π}{12}$)=-$\frac{\sqrt{2}}{2}$,且θ为锐角,则cos($\frac{π}{4}$-θ)的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
分析 法一:由已知根据角的范围,利用同角三角函数基本关系式可求sin(θ+$\frac{5π}{12}$)的值,由$\frac{π}{4}$-θ=(θ+$\frac{5π}{12}$)-$\frac{2π}{3}$,利用两角差的余弦函数公式即可计算得解.
法二:由已知利用三角函数恒等变换的应用化简可求2sin(2θ+$\frac{π}{3}$)=0,解得:θ=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z,结合θ为锐角,可得:θ=$\frac{π}{3}$,进而利用两角差的余弦函数公式及特殊角的三角函数值即可计算得解.
解答 解:法一:∵cos(θ+$\frac{5π}{12}$)=-$\frac{\sqrt{2}}{2}$,且θ为锐角,
∴θ+$\frac{5π}{12}$∈($\frac{5π}{12}$,$\frac{11π}{12}$),可得:sin(θ+$\frac{5π}{12}$)=$\sqrt{1-co{s}^{2}(θ+\frac{5π}{12})}$=$\frac{\sqrt{2}}{2}$,
∴cos($\frac{π}{4}$-θ)=cos[(θ+$\frac{5π}{12}$)-$\frac{2π}{3}$]=cos(θ+$\frac{5π}{12}$)cos$\frac{2π}{3}$+sin(θ+$\frac{5π}{12}$)sin$\frac{2π}{3}$=(-$\frac{\sqrt{2}}{2}$)×$(-\frac{1}{2})$+$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
法二:∵cos(θ+$\frac{5π}{12}$)=cos(θ+$\frac{π}{2}$-$\frac{π}{12}$)=-sin(θ-$\frac{π}{12}$)=-$\frac{\sqrt{2}}{2}$,
∴sin(θ-$\frac{π}{12}$)=$\frac{\sqrt{2}}{2}$,
∴sin(θ+$\frac{π}{4}$-$\frac{π}{3}$)=$\frac{1}{2}$sin(θ+$\frac{π}{4}$)-$\frac{\sqrt{3}}{2}$cos(θ+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,
∴化简可得:sinθ(1+$\sqrt{3}$)+cosθ(1-$\sqrt{3}$)=2,两边平方可得:sin2θ+$\sqrt{3}$cos2θ=0,
∴可得:2sin(2θ+$\frac{π}{3}$)=0,解得:θ=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z,
∵θ为锐角,可得:θ=$\frac{π}{3}$,
∴cos($\frac{π}{4}$-$\frac{π}{3}$)=cos$\frac{π}{4}$cos$\frac{π}{3}$+sin$\frac{π}{4}$sin$\frac{π}{3}$=$\frac{\sqrt{2}}{2}$×($\frac{1}{2}+\frac{\sqrt{3}}{2}$)=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
故选:D.
点评 本题主要考查了三角函数恒等变换在三角函数化简求值中的应用,考查了计算能力和转化思想,属于中档题.

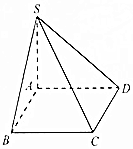 如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )
如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )| A. | 25π | B. | 50π | C. | 100π | D. | 200π |
| A. | $\sqrt{2}$ | B. | 1 | C. | 4 | D. | 2 |
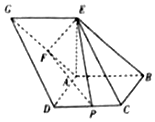 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE