题目内容
13.若命题:“?x∈R,使得ax2+(a-3)x+1<0”为假命题.则实数a的范围为( )| A. | 0<a≤1或a≥9 | B. | a≤1或a≥9 | C. | 1≤a≤9 | D. | a≥9 |
分析 依题意“?x∈R,使得ax2+(a-3)x+1≥0”恒成立.分a=0,a≠0讨论求解
解答 解:命题:“?x∈R,使得ax2+(a-3)x+1<0”为假命题?命题:“?x∈R,使得ax2+(a-3)x+1≥0”恒成立.
∵a=0时,不符合题意,
∴$\left\{\begin{array}{l}{a>0}\\{△=(a-3)^{2}-4a≤0}\end{array}\right.$
∴1≤a≤9
故选:C.
点评 本题考查了含有量词的命题真假的应用,转化思想是关键,属于基础题.

练习册系列答案
相关题目
2.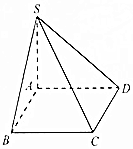 如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )
如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )
 如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )
如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )| A. | 25π | B. | 50π | C. | 100π | D. | 200π |
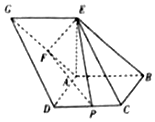 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE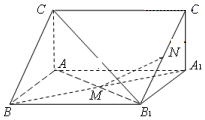 如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点
如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点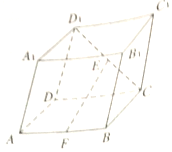 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为矩形,平面CDD1C1⊥平面ABCD,E,F分别是CD,AB的中点,求证:
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为矩形,平面CDD1C1⊥平面ABCD,E,F分别是CD,AB的中点,求证: