题目内容
在平面直角坐标系xoy中,o为坐标原点,A(sinωx,cosωx),B(cos
,sin
),ω>0.
(1)求证:向量
+
与
-
互相垂直;
(2)设函数f(x)=λ
•
(x∈R,λ为正实数),函数f(x)的图象上的最高点和相邻的最低点之间的距离为
,且f(x)的最大值为1,求函数f(x)的单调递增区间.
| π |
| 6 |
| π |
| 6 |
(1)求证:向量
| OA |
| OB |
| OA |
| OB |
(2)设函数f(x)=λ
| OA |
| OB |
| 5 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:综合题,三角函数的图像与性质
分析:(1)利用向量的数量积的坐标运算可求得(
+
)•(
-
)=0,从而可证
+
与
-
互相垂直;
(2)易求f(x)=λ
•
=λsin(ωx+
),依题意,λ=1,(
)2+[1-(-1)]2=(
)2,从而可求得T,继而可得ω,于是知f(x)=sin(πx+
),利用正弦函数的单调性即可求得
f(x)的单调递增区间.
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
(2)易求f(x)=λ
| OA |
| OB |
| π |
| 6 |
| T |
| 2 |
| 5 |
| π |
| 6 |
f(x)的单调递增区间.
解答:
解:(1)∵
=(sinωx,cosωx),
=(cos
,sin
),
∴|
|=1,|
|=1,
∴(
+
)•(
-
)=|
|2-|
|2=0,
∴
+
与
-
互相垂直;
(2)∵f(x)=λ
•
=λ(sinωxcos
+cosωxsin
)=λsin(ωx+
),
∵f(x)的最大值为1,
∴λ=1.
设f(x)的最小正周期为T,
由条件知,(
)2+[1-(-1)]2=(
)2,
∴
=
=1,T=2,ω=
=π,
∴f(x)=sin(πx+
),
令2kπ-
≤πx+
≤2kπ+
,
则2k-
≤x≤2k+
(k∈Z).
∴f(x)的单调递增区间为[2k-
,2k+
](k∈Z).
| OA |
| OB |
| π |
| 6 |
| π |
| 6 |
∴|
| OA |
| OB |
∴(
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
∴
| OA |
| OB |
| OA |
| OB |
(2)∵f(x)=λ
| OA |
| OB |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∵f(x)的最大值为1,
∴λ=1.
设f(x)的最小正周期为T,
由条件知,(
| T |
| 2 |
| 5 |
∴
| T |
| 2 |
(
|
| 2π |
| T |
∴f(x)=sin(πx+
| π |
| 6 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
则2k-
| 2 |
| 3 |
| 1 |
| 3 |
∴f(x)的单调递增区间为[2k-
| 2 |
| 3 |
| 1 |
| 3 |
点评:本题考查三角函数中的恒等变换应用,着重考查向量的数量积的坐标运算与正弦函数的单调性,求f(x)=λsin(ωx+
)的周期是难点,属于难题.
| π |
| 6 |

练习册系列答案
相关题目
一个空间几何体的三视图及其相关数据如图所示,则这个空间几何体的表面积是( )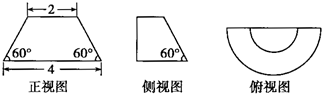

A、
| ||||
B、
| ||||
| C、11π | ||||
D、
|
若tanθ=2,则2sin2θ-sinθcosθ-cos2θ=( )
| A、5 | ||
| B、1 | ||
C、
| ||
D、
|
若直线l:4x+3y+a=0和圆C:x2+y2+2x-4y+1=0有公共点,则实数a的取值范围是( )
| A、[-12,8] |
| B、[-8,12] |
| C、[-22,18] |
| D、[-18,22] |
 已知几何体A-BCDE的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则该几何体的体积V的大小为
已知几何体A-BCDE的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则该几何体的体积V的大小为 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为