题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
)图象上某个最高点坐标为(2,
),由此最高点到相邻的最低点间函数图象与x轴交于一点(6,0).
(Ⅰ)求f(x)的解析式;
(Ⅱ)求使函数取最小值时x的取值集合;
(Ⅲ)求f(x)的单调区间.
| π |
| 2 |
| 2 |
(Ⅰ)求f(x)的解析式;
(Ⅱ)求使函数取最小值时x的取值集合;
(Ⅲ)求f(x)的单调区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:三角函数的图像与性质
分析:(Ⅰ)由函数的最值求出A,由周期求出ω,把定点坐标代入函数的解析式求得φ的值,从而求得函数的解析式
(Ⅱ)根据正弦函数的最值,求得y取得最大值和最小值,以及函数取最小值时x的取值集合.
(Ⅲ)令 2kπ-
≤
x+
≤2kπ+
,k∈z,求得x的范围,可得函数的增区间;令2kπ+
≤
x+
≤2kπ+
,求得x的范围,可得函数的减区间.
(Ⅱ)根据正弦函数的最值,求得y取得最大值和最小值,以及函数取最小值时x的取值集合.
(Ⅲ)令 2kπ-
| π |
| 2 |
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 8 |
| π |
| 4 |
| 3π |
| 2 |
解答:
解:(Ⅰ)由题意得T=4×(6-2)=16=
,所以ω=
,A=
,
将点(2,
)带入知函数f(x)=
sin(
x+φ),根据0<φ<
求得φ=
,
∴y=
sin(
x+
).
(Ⅱ)当
x+
=2kл+
,即x=16k+2,k∈z时,y取得最大为
;
当
x+
=2kл+
,即x=16k+10,k∈z时,y取得最小值为-
.
(Ⅲ)令 2kπ-
≤
x+
≤2kπ+
,k∈z,求得16k-6≤x≤16k+2,
故函数的增区间为[16k-6,16k+2];
令2kπ+
≤
x+
≤2kπ+
,k∈z时,求得16k+2≤x≤16k+10,
故函数的减区间为[16k+2,16k+10](k∈Z).
| 2π |
| ω |
| π |
| 8 |
| 2 |
将点(2,
| 2 |
| 2 |
| π |
| 8 |
| π |
| 2 |
| π |
| 4 |
∴y=
| 2 |
| π |
| 8 |
| π |
| 4 |
(Ⅱ)当
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
| 2 |
当
| π |
| 8 |
| π |
| 4 |
| 3π |
| 2 |
| 2 |
(Ⅲ)令 2kπ-
| π |
| 2 |
| π |
| 8 |
| π |
| 4 |
| π |
| 2 |
故函数的增区间为[16k-6,16k+2];
令2kπ+
| π |
| 2 |
| π |
| 8 |
| π |
| 4 |
| 3π |
| 2 |
故函数的减区间为[16k+2,16k+10](k∈Z).
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,把定点坐标代入函数的解析式求得φ的值,正弦函数的最值以及单调性,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知锐角三角形的边长分别为2,4,x,则x的取值范围是( )
A、1<x<
| ||||
B、
| ||||
C、1<x<2
| ||||
D、2
|
已知实数x,y满足方程x2+y2-4x+1=0,则
的取值范围是( )
| y |
| x+1 |
| A、[-1,1] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[0,
|
如果(x3-
)n的展开式中只有第4项的二项式系数最大,那么展开式中的所有项的系数和是( )
| 1 |
| 2x |
A、
| ||
| B、0 | ||
| C、64 | ||
| D、256 |
原点在直线l上的射影为点P(-2,1),则直线l的方程是( )
| A、x+2y=0 |
| B、2x+y+3=0 |
| C、x-2y+4=0 |
| D、2x-y+5=0 |
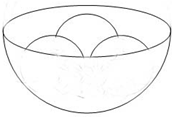 如图,三个半径都是10cm的小球放在一个半球面的碗中,小球的顶端恰好与碗的上沿处于同于水平面,则这个碗的半径R是
如图,三个半径都是10cm的小球放在一个半球面的碗中,小球的顶端恰好与碗的上沿处于同于水平面,则这个碗的半径R是