题目内容
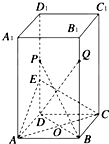 如图所示,已知正四棱柱ABCD-A1B1C1D1,点P为棱D1D的中点,且∠EOD=45°,AA1=2a,AB=a.
如图所示,已知正四棱柱ABCD-A1B1C1D1,点P为棱D1D的中点,且∠EOD=45°,AA1=2a,AB=a.(1)Q是BB1上一点,且BQ=
| 2 |
(2)试判断BP是否平行于平面EAC,并说明理由;
(3)若点M在侧面BB1C1C及其边界上运动,并且总保持AM⊥BP,试确定动点M所在位置.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)充分利用正四棱锥的性质可以证明AC⊥平面BD1.再利用线面垂直的性质 得到AC⊥DQ,进一步得到所证;
(2)BP不平行于平面EAC.利用反证法证明.
(3)取BB1中点G,连接CG,则M∈CG.由(1)知BP⊥AC,又取AA1、CC1中点R、S,连接PR、RG、GS、SP.
易证CG⊥平面BSP.得到CG⊥BP.于是BP⊥平面ACG.∴M∈CG
(2)BP不平行于平面EAC.利用反证法证明.
(3)取BB1中点G,连接CG,则M∈CG.由(1)知BP⊥AC,又取AA1、CC1中点R、S,连接PR、RG、GS、SP.
易证CG⊥平面BSP.得到CG⊥BP.于是BP⊥平面ACG.∴M∈CG
解答:
 (1)证明:∵ABCD-A1B1C1D1为正四棱柱,
(1)证明:∵ABCD-A1B1C1D1为正四棱柱,
∴AC⊥BD且AC⊥BB1,
∴AC⊥平面BD1.
又DQ⊆平面BD1,
∴AC⊥DQ.
又在Rt△EDO中,∠EOD=45°,OD=
a,
∴DE=
a.
又BQ=
a=BD,可得DQ⊥OE,
∴DQ⊥平面EAC.--------(4分)
(2)解:BP不平行于平面EAC.理由如下:
若BP∥平面EAC,又BP⊆DPB,平面DPB∩平面EAC=OE,∴BP∥OE.
又O为BD中点,则E为DP中点,这与DP=a,DE=
a矛盾,------------(9分)
(3)如图,取BB1中点G,连接CG,则M∈CG.
证明如下:
由(1)知BP⊥AC,又取AA1、CC1中点R、S,连接PR、RG、GS、SP.
可知ABCD-RGSP为正方体,易证CG⊥平面BSP.
∴CG⊥BP.
则BP⊥平面ACG.∴M∈CG.---------(14分)
 (1)证明:∵ABCD-A1B1C1D1为正四棱柱,
(1)证明:∵ABCD-A1B1C1D1为正四棱柱,∴AC⊥BD且AC⊥BB1,
∴AC⊥平面BD1.
又DQ⊆平面BD1,
∴AC⊥DQ.
又在Rt△EDO中,∠EOD=45°,OD=
| ||
| 2 |
∴DE=
| ||
| 2 |
又BQ=
| 2 |
∴DQ⊥平面EAC.--------(4分)
(2)解:BP不平行于平面EAC.理由如下:
若BP∥平面EAC,又BP⊆DPB,平面DPB∩平面EAC=OE,∴BP∥OE.
又O为BD中点,则E为DP中点,这与DP=a,DE=
| ||
| 2 |
(3)如图,取BB1中点G,连接CG,则M∈CG.
证明如下:
由(1)知BP⊥AC,又取AA1、CC1中点R、S,连接PR、RG、GS、SP.
可知ABCD-RGSP为正方体,易证CG⊥平面BSP.
∴CG⊥BP.
则BP⊥平面ACG.∴M∈CG.---------(14分)
点评:本题考查了线面平行和垂直的判定定理和性质定理的运用,关键是将所证转化为线线问题解答,体现了转化的数学思想.

练习册系列答案
相关题目
若双曲线C:
-
=1(a>0,b>0)的离心率e∈[
,
],则双曲线C的两条渐近线夹角的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| 2 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
P是边长1的正方形ABCD的对角线上一点,且
=λ
,则
•
≥
•
,则λ的取值范围( )
| BP |
| BD |
| CP |
| BP |
| PD |
| PD |
A、[[-
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|
“x2-x=0”是“x=0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |