Question

P是边长1的正方形ABCD的对角线上一点，且

BP

=λ

BD

，则

CP

•

BP

≥

PD

•

PD

，则λ的取值范围（　　）

• A、[[-

  1

  2

  ，1]
• B、[

  2- 2

  2

  ，1]
• C、[

  1

  2

  ，

  1+ 2

  2

  ]
• D、[

  1- 2

  2

  ，

  1+ 2

  2

  ]

Answer 1

考点：平面向量数量积的运算

专题：计算题,不等式的解法及应用,平面向量及应用

分析：以D为坐标原点，DA，DC所在直线为x，y轴建立直角坐标系，求出D，C，B的坐标，设P（x，y），则

DP

=（x，y），

DB

=（1，-1），运用向量的数量积的坐标表示，由条件列出不等式，注意0≤λ≤1，解出即可得到范围．

解答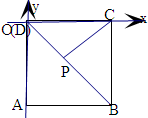： 解：以D为坐标原点，DA，DC所在直线为x，y轴建立直角坐标系，
则D（0，0），C（1，0），B（1，-1），
设P（x，y），则

DP

=（x，y），

DB

=（1，-1），
且

DP

=λ

DB

，则

DP

=（λ，-λ），

CP

=（λ-1，-λ），

PB

=（1-λ，-1+λ），
若

CP

•

DB

≥

PD

•

PB

，
则（λ-1，-λ）•（1，-1）≥（-λ，λ）•（1-λ，-1+λ），
即有λ-1+λ≥2λ（λ-1），即2λ²-4λ+1≤0，
解得，1-

2

2

≤λ≤1+

2

2

，
且0≤λ≤1，
即有1-

2

2

≤λ≤1，
故答案为：[1-

2

2

，1]．
故选B．

点评：本题考查平面向量的数量积的坐标表示，考查坐标法的运用，考查运算能力，属于中档题．