题目内容
在平面直角坐标系xOy中,F1、F2分别为椭圆C:
+
=1(a>b>0)的左、右焦点,B为短轴的一个端点,E是椭圆C上的一点,满足OE=OF1+
OB,且△EF1F2的周长为2(
+1).
(1)求椭圆C的方程;
(2)设点M是线段OF2上的一点,过点F2且与x轴不垂直的直线l交椭圆C于P、Q两点,若△MPQ是以M为顶点的等腰三角形,求点M到直线l距离的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(1)求椭圆C的方程;
(2)设点M是线段OF2上的一点,过点F2且与x轴不垂直的直线l交椭圆C于P、Q两点,若△MPQ是以M为顶点的等腰三角形,求点M到直线l距离的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知F1(-xc,0),设B(0,b),则E(-c,
b),
=
,2a+2c=2+2
,由此能求出椭圆C的方程.
(2)设点M(m,0),(0<m<1),直线l的方程为y=k(x-1),k≠0,由
,得:(1+2k2)x2-4k2x+2k2-2=0,由此利用韦达定理、中点坐标公式、点到直线的距离公式,结合已知条件能求出点M到直线距离的取值范围.
| ||
| 2 |
| c |
| a |
| ||
| 2 |
| 2 |
(2)设点M(m,0),(0<m<1),直线l的方程为y=k(x-1),k≠0,由
|
解答:
(本小题满分12分)
解:(1)由已知F1(-xc,0),设B(0,b),即
=(-c,0),
=(0,b),
∴
=(-c,
b),即E(-c,
b),
∴
+
=1,得
=
,①…(2分)
又△PF1F2的周长为2(
+1),
∴2a+2c=2+2
,②…(4分)
又①②得:c=1,a=
,∴b=1,
∴所求椭圆C的方程为:
+y2=1.…(5分)
(2)设点M(m,0),(0<m<1),直线l的方程为y=k(x-1),k≠0,
由
,消去y,得:(1+2k2)x2-4k2x+2k2-2=0,
设P(x1,y1),Q(x2,y2),PQ中点为N(x0,y0),
则x1+x2=
,∴y1+y2=k(x1+x2-2)=
,
∴x0=
=
,y0=
=
,
即N(
,
),…(8分)
∵△MPQ是以M为顶点的等腰三角形,∴MN⊥PQ,
即
=-1,
∴m=
=
∈(0,
),…(10分)
设点M到直线l:kx-y-k=0距离为d,
则d2=
=
<
=
,
∴d∈(0,
),
即点M到直线距离的取值范围是(0,
).…(12分)
解:(1)由已知F1(-xc,0),设B(0,b),即
| OF1 |
| OB |
∴
| OE |
| ||
| 2 |
| ||
| 2 |
∴
| c2 |
| a2 |
| ||
| b2 |
| c |
| a |
| ||
| 2 |
又△PF1F2的周长为2(
| 2 |
∴2a+2c=2+2
| 2 |
又①②得:c=1,a=
| 2 |
∴所求椭圆C的方程为:
| x2 |
| 2 |
(2)设点M(m,0),(0<m<1),直线l的方程为y=k(x-1),k≠0,
由
|
设P(x1,y1),Q(x2,y2),PQ中点为N(x0,y0),
则x1+x2=
| 4k2 |
| 1+2k2 |
| -2k |
| 1+2k2 |
∴x0=
| x1+x2 |
| 2 |
| 2k2 |
| 1+2k2 |
| y1+y2 |
| 2 |
| -k |
| 1+2k2 |
即N(
| 2k2 |
| 1+2k2 |
| -k |
| 1+2k2 |
∵△MPQ是以M为顶点的等腰三角形,∴MN⊥PQ,
即
| k2 |
| m(1+2k2)-2k2 |
∴m=
| k2 |
| 1+2k2 |
| 1 | ||
2+
|
| 1 |
| 2 |
设点M到直线l:kx-y-k=0距离为d,
则d2=
| k2(m-1)2 |
| k2+1 |
| k2(k2+1) |
| (1+2k2)2 |
| ||
| (1+2k2)2 |
| 1 |
| 4 |
∴d∈(0,
| 1 |
| 2 |
即点M到直线距离的取值范围是(0,
| 1 |
| 2 |
点评:本题考查椭圆方程的求法,考查点到直线的距离的取值范围的求法,解题时要认真审题,注意韦达定理、中点坐标公式、点到直线的距离公式的合理运用.

练习册系列答案
相关题目
以椭圆
+
=1的焦点为顶点,离心率为2的双曲线方程( )
| x2 |
| 25 |
| y2 |
| 16 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、以上都不对 |
已知点P是抛物线y2=4x上一点,设点P到此抛物线的准线的距离为d1,到直线x+2y-12=0的距离为d2,则d1+d2的最小值是( )
| A、5 | ||||
| B、4 | ||||
C、
| ||||
D、
|
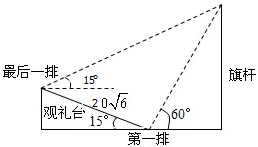 2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一垂直于地面的平面上,在该列的第一排B处和最后一排A处测得旗杆顶端的仰角为15°,且第一排和最后一排的距离为20
2009年北京国庆阅兵式上举行升旗仪式,如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一垂直于地面的平面上,在该列的第一排B处和最后一排A处测得旗杆顶端的仰角为15°,且第一排和最后一排的距离为20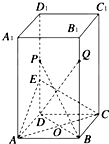 如图所示,已知正四棱柱ABCD-A1B1C1D1,点P为棱D1D的中点,且∠EOD=45°,AA1=2a,AB=a.
如图所示,已知正四棱柱ABCD-A1B1C1D1,点P为棱D1D的中点,且∠EOD=45°,AA1=2a,AB=a.