题目内容
函数γ=esinx(-π≤x≤π)的图象大致是 .
考点:函数的图象
专题:函数的性质及应用
分析:根据复合函数求出函数的单调区间,最值和端点值,和特殊点,画出图象即可
解答:
 解:因为函数γ=eu为指数函数,恒过点(0,1),且为增函数,
解:因为函数γ=eu为指数函数,恒过点(0,1),且为增函数,
而u=sinx在(-
,
)为增函数,在[-π,-
]和[
,π]为减函数,
故函数γ=esinx(-
,
)为增函数,在[-π,-
]和[
,π]为减函数,
且在x=-
时,函数有最小值,最小值为y=
,
且在x=
时,函数有最大值,最小值为y=e,
函数的端点值为f(π)=1.f(-π)=1,
故做出函数的图象如图所示
故答案为:如图所示
 解:因为函数γ=eu为指数函数,恒过点(0,1),且为增函数,
解:因为函数γ=eu为指数函数,恒过点(0,1),且为增函数,而u=sinx在(-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故函数γ=esinx(-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
且在x=-
| π |
| 2 |
| 1 |
| e |
且在x=
| π |
| 2 |
函数的端点值为f(π)=1.f(-π)=1,
故做出函数的图象如图所示
故答案为:如图所示
点评:本题考查了函数图象的画法,属于中档题

练习册系列答案
相关题目
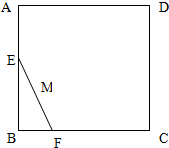 如图,线段EF的长度为1,端点E、F在边长不小于1的正方形ABCD的四边上滑动,当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为L,其围成的面积为S,则L-S的最大值为( )
如图,线段EF的长度为1,端点E、F在边长不小于1的正方形ABCD的四边上滑动,当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为L,其围成的面积为S,则L-S的最大值为( )| A、4-π | ||
B、2+
| ||
C、
| ||
| D、2π-2 |
下列各式错误的是( )
| A、tan138°<tan143° | ||||
B、sin(-
| ||||
| C、lg1.6>lg1.4 | ||||
| D、0.75-0.1<0.750.1 |
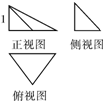 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )| A、36π | ||
| B、9π | ||
C、
| ||
D、
|
已知某几何体的三视图如上图所示(单位:cm),则该几何体的表面积是( )
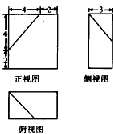

A、(124+2
| ||
| B、92cm2 | ||
| C、124cm2 | ||
| D、84cm2 |
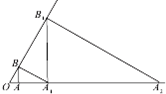 如图,在△OAB中,OA⊥AB,OB=1,OA=
如图,在△OAB中,OA⊥AB,OB=1,OA=