题目内容
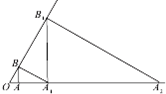 如图,在△OAB中,OA⊥AB,OB=1,OA=
如图,在△OAB中,OA⊥AB,OB=1,OA=| 1 |
| 2 |
考点:归纳推理
专题:等差数列与等比数列,推理和证明
分析:根据已知,求出△OAB的面积为al,△O A1B的面积为a2,△OA1B1的面积为a3,…,进而可得数列{an}是一个以
为首项,以4为公比的等比数列,进而得到答案.
| ||
| 8 |
解答:
解:∵在△OAB中,OA⊥AB,OB=1,OA=
,过B点作OB延长线的垂线交OA延长线于点A1,
∴△OAB的面积a1=
,
过点A1作OA延长线的垂线交OB延长线于点B1,
∴△O A1B的面积a2=
,
如此继续下去,△OA1B1的面积a3=2
,
…,
则数列{an}是一个以
为首项,以4为公比的等比数列,
∴an=
•4n-1,
∴a6=128
.
故答案为:128
| 1 |
| 2 |
∴△OAB的面积a1=
| ||
| 8 |
过点A1作OA延长线的垂线交OB延长线于点B1,
∴△O A1B的面积a2=
| ||
| 2 |
如此继续下去,△OA1B1的面积a3=2
| 3 |
…,
则数列{an}是一个以
| ||
| 8 |
∴an=
| ||
| 8 |
∴a6=128
| 3 |
故答案为:128
| 3 |
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
已知R是实数集,集合M={x|
<1},N={y|y=x+
},则N∩(∁RM)=( )
| 3 |
| x |
| x-2 |
| A、[0,2] |
| B、[2,+∞) |
| C、(-∞,2] |
| D、[2,3] |
若f(x)=
,则f(-8)等于( )
| x | ||
|
A、-
| ||
B、-
| ||
C、
| ||
D、±
|