题目内容
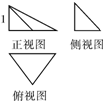一个几何体的三视图如图所示，其中俯视图是一个腰长为2的等腰直角三角形，则该几何体外接球的体积是（ ）| A、36π | ||
| B、9π | ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知中的三视图可得该几何体是一个三棱锥，求出底面外接圆半径和棱锥的高，进而利用勾股定理，求出其外接球的半径，代入球的体积公式，可得答案．
解答：
解：∵俯视图是一个腰长为2的等腰直角三角形，
故底面外接圆半径r=
，
由主视图中棱锥的高h=1，
故棱锥的外接球半径R满足：R=
=
，
故该几何体外接球的体积V=
πR3=
π，
故选：C
故底面外接圆半径r=
| 2 |
由主视图中棱锥的高h=1，
故棱锥的外接球半径R满足：R=
(
|
| 3 |
| 2 |
故该几何体外接球的体积V=
| 4 |
| 3 |
| 9 |
| 2 |
故选：C
点评：解决三视图的题目，关键是由三视图判断出几何体的形状及度量长度，进而求出外接球半径，是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
在平面直角坐标系xOy中，已知P是函数f（x）=lnx（x＞1）的图象上的动点，该图象在点p处的切线l交x轴于点M．过点P作l的垂线交x轴于点N，设线段MN的中点的横坐标为t，则t的最大值是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
| D、1 |