题目内容
在正方体ABCD-A1B1C1D1中,棱AA1上有一动点M,棱BD1上有一动点N,当MN⊥AA1时,棱长为a.问:线段MN的最小值为多少?
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:线段MN的最小值为异面直线AA1与BD1的距离.
解答:
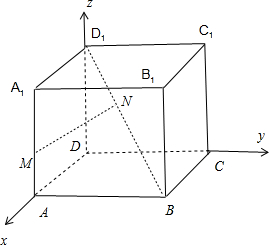 解:以D为原点,建立空间直角坐标系D-xyz,
解:以D为原点,建立空间直角坐标系D-xyz,
A(a,0,0),A1(a,0,a),B(a,a,0),D1(0,0,a),
=(0,0,a),
=(a,a,-a),
=(0,a,0),
设
和
的公共法向量
=(x,y,z),
∴
,
取x=1,得
=(1,-1,0),
∴异面直线AA1与BD1的距离d=
=
.
∴线段MN的最小值为
.
 解:以D为原点,建立空间直角坐标系D-xyz,
解:以D为原点,建立空间直角坐标系D-xyz,A(a,0,0),A1(a,0,a),B(a,a,0),D1(0,0,a),
| AA1 |
| D1B |
| AB |
设
| AA1 |
| D1B |
| n |
∴
|
取x=1,得
| n |
∴异面直线AA1与BD1的距离d=
|
| ||||
|
|
| ||
| 2 |
∴线段MN的最小值为
| ||
| 2 |
点评:本题考查线段的最小值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
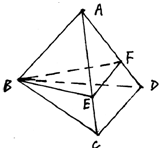 已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求:
已知正三棱锥A-BCD中,底面边长为a,侧棱长为2a,过B点作与则棱AC、AD相交的截面BEF,在这个截面三角形中,求: 已知三棱锥A-BCD中,侧棱长和底面边长均相等,E为侧棱AB的中点,求证:
已知三棱锥A-BCD中,侧棱长和底面边长均相等,E为侧棱AB的中点,求证: