题目内容
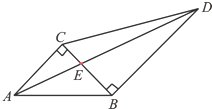如图，两块直角三角板拼在一起，已知∠ABC=45°，∠BCD=60°．（1）若记
| AB |
| a |
| AC |
| b |
| a |
| b |
| AD |
| CD |
（2）若AB=
| 2 |
| AD |
| AB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）利用向量的三角形法则、共线定理即可得出．
（2）利用数量积的定义及其运算性质即可得出．
（2）利用数量积的定义及其运算性质即可得出．
解答：
解：（1）
=
-
，
∵AC∥BD，BD=
BC=
BD．
∴
=
，
则
=
+
=
+
，
=
-
=
+(
-1)
．
（2）∵
•
=1×
cos45°=1．
∴
•
=(
+
)•
=
2+
=2+
．
| CB |
| a |
| b |
∵AC∥BD，BD=
| 3 |
| 3 |
∴
| BD |
| 3 |
| b |
则
| AD |
| AB |
| BD |
| a |
| 3 |
| b |
| CD |
| AD |
| AC |
| a |
| 3 |
| b |
（2）∵
| a |
| b |
| 2 |
∴
| AD |
| AB |
| a |
| 3 |
| b |
| a |
| a |
| 3 |
| a• |
| b |
| 3 |
点评：本题考查了向量的三角形法则、共线定理、数量积的定义及其运算性质，属于基础题．
练习册系列答案
相关题目
函数y=
的值域是（ ）
| 2x+1 |
| x-3 |
| A、（-∞，3）∪（3，+∞） |
| B、（-∞，2）∪（2，+∞） |
| C、R |
| D、（-∞，2）∪（3，+∞） |
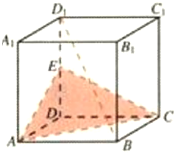如图在正方体ABCD-A1B1C1D1中，AA1=2，E是DD1的中点，