题目内容
已知函数f(x)=-x3+ax2+bx+c在(-∞,0)上是减函数,在(0,1)上是增函数,函数f(x)在R上有三个零点.
(1)求b的值;
(2)若1是其中一个零点,求f(2)的取值范围.
(1)求b的值;
(2)若1是其中一个零点,求f(2)的取值范围.
考点:函数零点的判定定理,利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求导,由极值的定义确定b的值;(2)代入零点确定a与c的关系,求出取值范围.
解答:
解:(1)∵f(x)=-x3+ax2+bx+c,
∴f′(x)=-3x2+2ax+b.
∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,
∴当x=0时,f(x)取到极小值,即f′(0)=0.
∴b=0.
(2)解:由(1)知,f(x)=-x3+ax2+c,
∵1是其中一个零点,则f(1)=-1+a+c=0,
∴c=1-a.
∵f′(x)=-3x2+2ax=0的两根为0,
;
∵f(x)在(0,1)上是增函数,且函数f(x)在R上有三个零点,
∴
>1,即a>
.
∴f(2)=3a-7>-
.
故f(2)的取值范围为(-
,+∞).
∴f′(x)=-3x2+2ax+b.
∵f(x)在(-∞,0)上是减函数,在(0,1)上是增函数,
∴当x=0时,f(x)取到极小值,即f′(0)=0.
∴b=0.
(2)解:由(1)知,f(x)=-x3+ax2+c,
∵1是其中一个零点,则f(1)=-1+a+c=0,
∴c=1-a.
∵f′(x)=-3x2+2ax=0的两根为0,
| 2a |
| 3 |
∵f(x)在(0,1)上是增函数,且函数f(x)在R上有三个零点,
∴
| 2a |
| 3 |
| 3 |
| 2 |
∴f(2)=3a-7>-
| 5 |
| 2 |
故f(2)的取值范围为(-
| 5 |
| 2 |
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
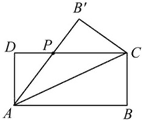 设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.
设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.