题目内容
若α∈(0,
),β∈(0,π)且tan(a-β)=
,tanβ=-
,则2α-β( )
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
考点:两角和与差的正切函数
专题:三角函数的求值
分析:首先,求解tanα=
,然后,根据2α-β=(α-β)+α,求解tan(2α-β)=tan[(α-β)+α]=1,最后,结合2α-β∈(-π,0),从而确定2α-β的值.
| 1 |
| 3 |
解答:
解:∵tanα=tan[(α-β)+β]=
=
=
,
∴tanα=
.
∵tan(2α-β)=tan[(α-β)+α]=
=
=1.
∵α∈(0,
),β∈(0,π)
∵tanβ=-
<0,
∴β∈(
,π)
∴2α-β∈(-π,0),
∴2α-β=-
.
故选:D.
| tan(α-β)+tanβ |
| 1-tan(α-β)tanβ |
| ||||
1+
|
| 1 |
| 3 |
∴tanα=
| 1 |
| 3 |
∵tan(2α-β)=tan[(α-β)+α]=
| tan(α-β)+tanα |
| 1-tan(α-β)tanα |
| ||||
1-
|
∵α∈(0,
| π |
| 4 |
∵tanβ=-
| 1 |
| 7 |
∴β∈(
| π |
| 2 |
∴2α-β∈(-π,0),
∴2α-β=-
| 3π |
| 4 |
故选:D.
点评:本题重点考查了两角和与差的正切公式,掌握公式的运用是解题的关键,属于中档题.

练习册系列答案
相关题目
下列说法错误的是( )
| A、数据1,2,3,4,5的平均数、众数、中位数都是3 | ||||||||
| B、若命题p∧q为真命,则p∨q为真 | ||||||||
| C、若p:?x∈R,x2-x+1>0,则¬p:?x0∈R,x02-x0+1≤0 | ||||||||
D、“若α=
|
已知动点P(a,b)在不等式组
表示的平面区域内部运动,则
的取值范围是( )
|
| b+3 |
| a-1 |
A、(-
| ||
| B、(-3,2) | ||
C、(-∞,-
| ||
| D、(1,3) |
把1100(2)化为十进制数,则此数为( )
| A、8 | B、12 | C、16 | D、20 |
若(9x-
)n(n∈N*)的展开式的第3项的二项式系数为36,则其展开式中的常数项为( )
| 1 | ||
3
|
| A、252 | B、-252 |
| C、84 | D、-84 |
cos
+tan(-
)+sin21π的值为( )
| 9π |
| 4 |
| 7π |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知定义域为R的奇函数f(x)的导函数为f′(x),当x≠0时,f′(x)+
>0,若a=
f(
),b=-2f(-2),c=(ln
)f(ln
),则a,b,c的大小关系正确的是( )
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<c<b |
| B、b<c<a |
| C、a<b<c |
| D、c<a<b |
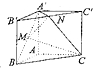 如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=