题目内容
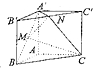 如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=
如图,直三角棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=| 2 |
(1)证明:MN∥平面A′ACC′;
(2)求平面A′MN与平面MNC的夹角.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)连接AB′、AC′,说明三棱柱ABC-A′B′C′为直三棱柱,推出MN∥AC′,然后证明MN∥平面A′ACC′;
(2)建立直角坐标系,求出平面A′MN的法向量、平面MNC的法向量,利用向量的夹角公式,即可求出平面A′MN与平面MNC的夹角.
(2)建立直角坐标系,求出平面A′MN的法向量、平面MNC的法向量,利用向量的夹角公式,即可求出平面A′MN与平面MNC的夹角.
解答:
(1)证明:连接AB′、AC′,
由已知∠BAC=90°,AB=AC,
三棱柱ABC-A′B′C′为直三棱柱,
所以M为AB′中点,
又因为N为B′C′的中点,
所以MN∥AC′,
又MN?平面A′ACC′,
因此MN∥平面A′ACC′;
(2)解:以A为坐标原点,分别以直线AB、AC、AA′为x,y,z轴,建立直角坐标系,如图,
A(0,0,0),B(
,0,0),C(0,
,0),A′(0,0,1),B′(
,0,1),C′(0,
,1).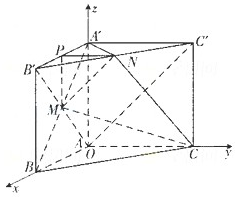
所以M(
,0,
),N(
,
,1),
设
=(x1,y1,z1)是平面A′MN的法向量,
由
,得
,得
=(1,-1,
),
同理平面MNC的法向量
=(-3,-1,
),
所以
•
=0
所以平面A′MN与平面MNC的夹角为90°.
由已知∠BAC=90°,AB=AC,
三棱柱ABC-A′B′C′为直三棱柱,
所以M为AB′中点,
又因为N为B′C′的中点,
所以MN∥AC′,
又MN?平面A′ACC′,
因此MN∥平面A′ACC′;
(2)解:以A为坐标原点,分别以直线AB、AC、AA′为x,y,z轴,建立直角坐标系,如图,
A(0,0,0),B(
| 2 |
| 2 |
| 2 |
| 2 |

所以M(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
设
| m |
由
|
|
| m |
| 2 |
同理平面MNC的法向量
| n |
| 2 |
所以
| m |
| n |
所以平面A′MN与平面MNC的夹角为90°.
点评:本题以三棱柱为载体主要考查空间中的线面平行的判定,借助空间直角坐标系求平面的法向量的方法,并利用法向量判定平面的垂直关系,考查空间想象能力、推理论证能力、运算求解能力,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若α∈(0,
),β∈(0,π)且tan(a-β)=
,tanβ=-
,则2α-β( )
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
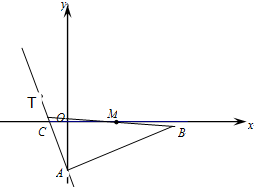 如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0).
如图,在Rt△ABC中,∠A为直角,AB边所在直线的方程为x-3y-6=0,点T(-1,1)在直线AC上,斜边中点为M(2,0). 在圆内接四边形ABCD中,AC与BD交于点E,过点A作圆的切线交CB的延长线于点F.若AB=AD,AF=18,BC=15,求AE的长.
在圆内接四边形ABCD中,AC与BD交于点E,过点A作圆的切线交CB的延长线于点F.若AB=AD,AF=18,BC=15,求AE的长.