题目内容
下列说法错误的是( )
| A、数据1,2,3,4,5的平均数、众数、中位数都是3 | ||||||||
| B、若命题p∧q为真命,则p∨q为真 | ||||||||
| C、若p:?x∈R,x2-x+1>0,则¬p:?x0∈R,x02-x0+1≤0 | ||||||||
D、“若α=
|
考点:命题的真假判断与应用
专题:综合题
分析:A中,根据平均数、众数和中位数的定义,判定A正确;
B中,根据命题p∧q与p∨q的真假性,判定B正确;
C中,根据全称命题p的否定是特称命题¬p,判定C正确;
D中,根据原命题与否命题的关系判定D错误.
B中,根据命题p∧q与p∨q的真假性,判定B正确;
C中,根据全称命题p的否定是特称命题¬p,判定C正确;
D中,根据原命题与否命题的关系判定D错误.
解答:
解:对于A,数据1,2,3,4,5中的每一个数据出现的次数都相等,都是众数;再根据平均数、中位数的定义,得出A正确;
对于B,命题p∧q为真命题时,p、q都是真命题,∴p∨q是真命题,∴B正确;
对于C,命题p是“?x∈R,x2-x+1>0”,它的否定是¬p:?x0∈R,x02-x0+1≤0,∴C正确;
对于D,命题若α=
,则tanα=
的否命题是若α≠
,则tanα≠
,∴D错误.
所以,符合题意的是D选项.
故选:D.
对于B,命题p∧q为真命题时,p、q都是真命题,∴p∨q是真命题,∴B正确;
对于C,命题p是“?x∈R,x2-x+1>0”,它的否定是¬p:?x0∈R,x02-x0+1≤0,∴C正确;
对于D,命题若α=
| π |
| 3 |
| 3 |
| π |
| 3 |
| 3 |
所以,符合题意的是D选项.
故选:D.
点评:本题通过命题真假的判定,考查了平均数、众数和中位数的求法,复合命题的判定,命题的否定以及原命题与否命题等知识,是基础题目.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
某程序的框图如图所示,执行该程序,若输入的E为0.96,则输出的K为( )


| A、20 | B、22 | C、24 | D、25 |
已知函数f(x)=sin(ωx+
)(ω>0),若存在实数x0使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2013)成立,则ω的最小值是( )
| π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知i是虚数单位,复数
=1-bi,其中a、b∈R,则|a+bi|等于( )
| 2-ai |
| i |
| A、-1+2i | ||
| B、1 | ||
C、
| ||
| D、5 |
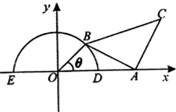 如图,半圆的圆心在直角坐标原点,点A,D,E的坐标分别为A(2,0),D(1,0),E(-1,0),且点B在半圆上自点D逆时针向点E运动,三角形ABC是等腰直角三形,∠BAC是直角,则四边形OACB的面积的最大值是( )
如图,半圆的圆心在直角坐标原点,点A,D,E的坐标分别为A(2,0),D(1,0),E(-1,0),且点B在半圆上自点D逆时针向点E运动,三角形ABC是等腰直角三形,∠BAC是直角,则四边形OACB的面积的最大值是( )A、
| ||||
B、2+2
| ||||
C、
| ||||
D、2+
|
若α∈(0,
),β∈(0,π)且tan(a-β)=
,tanβ=-
,则2α-β( )
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
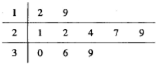 某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )
某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )