题目内容
把1100（2）化为十进制数，则此数为（ ）
| A、8 | B、12 | C、16 | D、20 |
考点：进位制,整除的定义
专题：算法和程序框图
分析：利用“2进制”与“十进制”之间的换算关系即可得出．
解答：
解：1100（2）=1×23+1×22+0×21+0×20=12．
故选：B．
故选：B．
点评：本题考查了“2进制”与“十进制”之间的换算关系，属于基础题．
练习册系列答案
相关题目
某程序的框图如图所示，执行该程序，若输入的E为0.96，则输出的K为（ ）
| A、20 | B、22 | C、24 | D、25 |
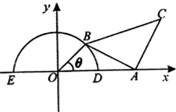如图，半圆的圆心在直角坐标原点，点A，D，E的坐标分别为A（2，0），D（1，0），E（-1，0），且点B在半圆上自点D逆时针向点E运动，三角形ABC是等腰直角三形，∠BAC是直角，则四边形OACB的面积的最大值是（ ）A、
| ||||
B、2+2
| ||||
C、
| ||||
D、2+
|
在复平面内，复数z和（2-i）i表示的点关于虚轴对称，则复数z=（ ）
| A、1+2i | B、-1+2i |
| C、-1-2i | D、1-2i |
已知sinxcosy=
，则cosxsiny的取值范围是（ ）
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
| D、[-1，1] |
若α∈（0，
），β∈（0，π）且tan（a-β）=
，tanβ=-
，则2α-β（ ）
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 7 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
已知平面向量
，
满足|
|=1，|
|=2，且（
-
）⊥
，则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|